Multiple Choice Questions
Instructions: For each of the following questions, select the “best” answer and
darken the corre-
sponding oval on your scantron. Good luck!
1. One of the zeros of f(x) = x2-4x-6 is
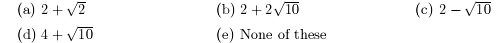
2. The function f(x) = x3+x-3 is
(a) even (b) odd (c) neither even nor odd
3. Fina all values of k so that kx2-3x-8 = 0 has exactly one real
root.
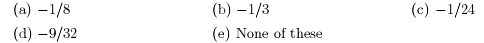
4. Simplify the complex number
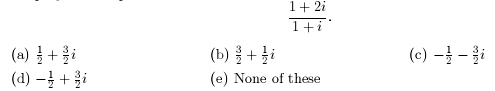
5. Consider the function

The function f has a zero at
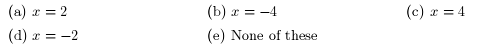
6. The function ƒ of Exercise 5 has a vertical asymptote
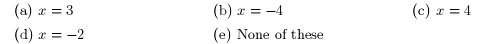
7. The function ƒ of Exercise 5 has a horizontal asymptote
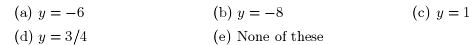
8. The function

has an oblique asymptote
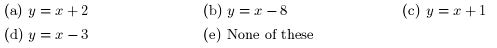
Instructions. Please place the solution of each of the following questions on
graph paper. You
must show all supporting work to receive credit for your solution. Please note
that there are six
exercises in this section.
Exercise 1. Using hand calculations only, provide an algebraic solution of the
inequality

Shade your solution on a number line, then use both interval and set-builder
notation to describe
your solution set.
Exercise 2. Solve the equation

for T.
Exercise 3. Given the function f(x) = x2+5x, simply the expression

as much as possible.
Exercise 4. Using hand calculations only, present an algebraic solution of the
radical equation

Remember to check your solutions.
Exercise 5. Consider the quadratic function
f(x) = x2-8x-9.
Perform each of the following tasks on graph paper.
(a) Use the method of completing the square to put the quadratic equation in
vertex form. Plot
and label the vertex with its coordinates. Draw the axis of symmetry and label
it with its
equation.
(b) Use a strictly algebraic approach (no calculators) to find the x- and
y-intercepts of the quadratic
function f. Plot and label each intercept with its coordinates. You must show
your work to
receive credit for this part.
(c) Sketch the graph of f using all of the information in parts (a) and (b). Use
interval notation
to describe the domain and range of the function f.
Exercise 6. Consider the rational function

Complete each of the following tasks.
(a) Set up a coordinate system on graph paper, then plot the x-intercepts of the
rational function
f and label each with its coordinates.
(b) Plot the vertical asymptotes of the rational function f and label each with
its equation.
(c) Perform the appropriate computation (using limit notation) to deduce the
equation of any
horizontal asymptote(s). Plot the resulting asymptote(s) on your coordinate
system and label
each with its equation.
(d) Set up a number line and place the x-values that produce zeros or vertical
asymptotes on your
number line. Evaluate the function at a point from each interval delimited by
these x-values.
Plot the results on your coordinate system.
(e) Sketch the rational function ƒ on your coordinate system using the
information from parts
(a)-(c) above.
(f) Shade the solution of f(x) ≥ 0 on the x-axis of your coordinate system, then
describe this
solution using interval notation.


