Math 222 - Lecture 1

Power series: everyones favorite functions are polynomials!

Unpacking the concepts:
(this stuff might look familiar, but it's good to go through).

1. For what x does
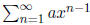converge? converge conditionally? converge absolutely?
What kind of series is this?

2. For those x for whichconverges, what does it converge to?

3. For each of the following x's,

(i) estimate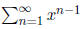by calculating the first few partial sums.

(ii) what is?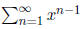

(iii) how far out in the sequence of partial sums do you have to go to get within 1=100
of the actual value?

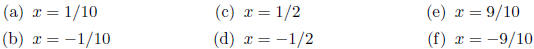
Conjecture: the sequence of partial sums ofconverge faster when____ .

4. Turn to page 799 in your book, and read up on testing for convergence. For what x
to the following series converge absolutely? converge conditionally? diverge?

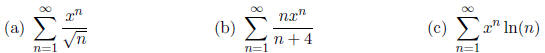
5. I have a secret function in a box, about which I claim two things: (1) it can me written
as an infinite power series, and (2) when I take it's derivative, I get the function back

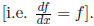
(a) What is this super secret series? (Hint: all power series look like

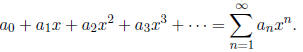
Take this thing's derivative and set it equal to the series and solve for the coef-
ficients . Look for patterns.)

(b) For what x does this series converge?

(c) What's another function you know which satisfies part (2)?

(d) For those x which causes this series to converge, what does it converge to?

6. e is irrational. Recall that a rational number is one which can be written as the
ratio of integers, and that an irrational number is one that can't. In general, proving
that a number is rational is a lot easier than proving that it isn't| the former just
requires you to find the appropriate fraction, whereas the latter can't be done by
example (you can't try all possibilities, since there are infinitely many!!).

Use the series expansion of e^x to prove that 1/e is not rational, and therefore neither
is e.

(hint:

(a) Assume you can write e as p/q, where p and q are integers, and are reduced
(there are no factors that p and q have in common. So what's 1/e?

(b) Plug in x = -1 into the series expansion for e^x, and use some partial sum
to estimate 1/e. What kind of series do you get? What's the error of your
estimate? What does that mean about the distance between q/p and s_n? Write
this inequality down.

(c) You can pick an n large enough so that there is something you can multiply both
sides by to get integers on both sides. How large does n have to be? How do you
clear all the fractions in a useful way? What can you conclude?

(d) Find a contradiction of your assumption in part (a). What does this mean? )

7. The other day, as Ruth and Zajj were cleaning up, an alien appeared in the WES
classroom. The alien told them \I'm thinking of two integers, both bigger than 3 and
smaller than 97. I will tell their sum to Ruth and their product to Zajj." The alien
did this and then disappeared. The following conversation occurred.
Ruth: You dont know what the numbers are.
Zajj: Well, I didn't, but now I do.
Ruth: Now I do too!

Assuming Zajj and Ruth weren't using their psychic powers, determine what the two
integers were.