Polynomials
17.11 Show that x4 + 1 is irreducible over Q but
reducible over R.
Note that f(x) = x4 + 1 is irreducible over Q if
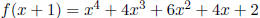 is
is
irreducible over Q. By Eisenstein’s Criterion, f(x + 1) is irreducible over Q
(consider the prime
p = 2), and so f(x) = x4 + 1 is irreducible over Q.
Observe that over R, 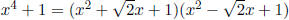 . Note that each of these degree
. Note that each of these degree
two factors is irreducible, for if one of them were reducible, x4 + 1 would have
a linear factor (i.e.
a root) over R, which is clearly not the case.
17.17 Show that for every prime p there exists a field of order p2.
We will show that an irreducible polynomial of degree two always exists over
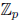 .
A reducible
.
A reducible
monic quadratic polynomial has the form (x −α )(x − β). There are p monic
polynomials of
degree one over 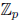 , and so there are p(p − 1)/2 + p = p(p + 1)/2 (consider the
case α= β)
, and so there are p(p − 1)/2 + p = p(p + 1)/2 (consider the
case α= β)
reducible monic polynomials of degree two over 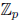 . But p(p + 1)/2 < p2, where p2
is the number
. But p(p + 1)/2 < p2, where p2
is the number
of monic quadratic polynomials over 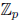 . Therefore, there always exists a (monic)
irreducible
. Therefore, there always exists a (monic)
irreducible
polynomial f(x) of degree two over 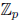 , and so
, and so
 is a finite field of
order p2.
is a finite field of
order p2.
17.24 Find all zeros of f(x) = 3x2 +x+4 over
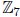 by substitution. Find all zeros
of f(x) by using
by substitution. Find all zeros
of f(x) by using
the Quadratic Formula  . Do your answers agree? Should they? Find all
. Do your answers agree? Should they? Find all
zeros of g(x) = 2x2 + x + 3 over 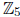 by substitution. Try the Quadratic Formula
on g(x). Do your
by substitution. Try the Quadratic Formula
on g(x). Do your
answers agree? State necessary and sufficient conditions for the Quadratic
Formula to yield the
zeros of a quadratic from 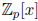 , where p is a prime greater than 2.
, where p is a prime greater than 2.
For f(x), both methods give the zeros 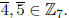 Note that the quadratic formula
involves the
Note that the quadratic formula
involves the
term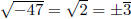 in
in 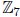 . We do not find any zeros for g(x). In this case, the quadratic
. We do not find any zeros for g(x). In this case, the quadratic
formula produces the term 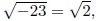 and
and
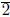 is not a square in
is not a square in
![]() , i.e. there is no element
, i.e. there is no element
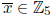 such that
such that  (mod 5).
(mod 5).
A quadratic polynomial ax2 + bx + c (a ≠ 0) has a zero in
![]() if and only if
its discriminant
if and only if
its discriminant
is a square in 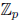 , i.e.
, i.e.
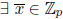 such that
such that 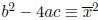 (mod p).
(mod p).
17.25 (Rational Root Theorem) Let 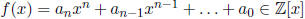 and
and
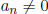 . Prove
. Prove
that if r and s are relatively prime integers and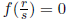 , then
, then
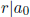 and
and 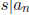 .
.
If 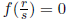 , then
, then 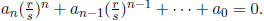 Multiplying both sides by sn, we have
Multiplying both sides by sn, we have
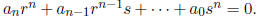 Since r divides every term except
Since r divides every term except
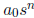 and (r,
s) = 1, we must
and (r,
s) = 1, we must
have ![]() . Since s divides every term except for
. Since s divides every term except for
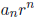 and (r, s) = 1, we must
have
and (r, s) = 1, we must
have ![]() .
.
17.29 Show that x4 + 1 is reducible over 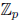 for every prime p.
for every prime p.
We will show that for every prime p, at least one of the elements
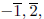 or
or 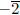 is square in
is square in 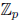 .
.
This will give us the desired result since:
If 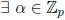 such that
such that
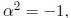 then
then 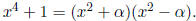
If 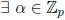 such that
such that
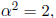 then
then 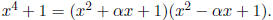
If 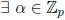 such that
such that
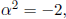 then
then 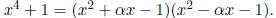
To see that one of these cases must hold, consider the homomorphism
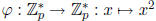
Since 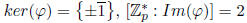 (this argument does not hold for p = 2, but this case can
(this argument does not hold for p = 2, but this case can
be handled separately). Suppose that 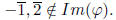 Since
Since
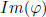 only has two cosets in
only has two cosets in
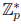 , we
, we
have 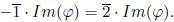 Additionally,
Additionally,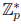 is abelian,
and so
is abelian,
and so 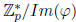 is a group. Note that
is a group. Note that
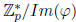 has order 2, so the square of any element in this factor group is the
identity coset
has order 2, so the square of any element in this factor group is the
identity coset
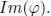 Now we have
Now we have
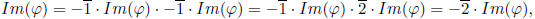 so
so
that 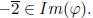 Therefore,
Therefore,
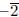 is a square in
is a square in
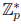 , so one of the three desired cases holds in
, so one of the three desired cases holds in
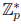
for all primes p.


