Polynomials, Polynomial Functions, and Factoring
§ 5.1
Introduction to Polynomials and Polynomial
Functions
Polynomials
A polynomial is a single term or the sum of two or more
terms containing variables with whole number exponents.
Consider the polynomial: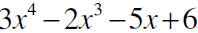
This polynomial contains four terms. It is customary to
write the terms in
order of descending powers of the variable. This is the standard form of a
polynomial.
The degree of a polynomial is the greatest degree of any
term
of the polynomial. The degree of a term 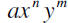 is
(n +m)
is
(n +m)
and the coefficient of the term is a. If there is exactly
one
term of greatest degree, it is called the leading term. It’ s
coefficient is called the leading coefficient. Consider the
polynomial: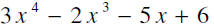
3 is the leading coefficient. The degree is 4.
The Degree of
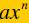 If 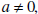 the degree of the degree of
 is n. The degree of a is n. The degree of anonzero constant is 0. The constant 0 has no defined degree. |
| Adding Polynomials Polynomials are added by removing the parentheses that surround each polynomial (if any) and then combining like terms. |
| Subtracting Polynomials To subtract two polynomials, change the sign of every term of the second polynomial. Add this result to the first polynomial. |
EXAMPLE
Determine the coefficient of each term, the degree of each
term, the degree of the polynomial, the leading term, and the
leading coefficient of the polynomial.

SOLUTION

CONTINUED
The degree of the polynomial is the greatest degree of all
its
terms, which is 10. The leading term is the term of the
greatest degree, which is 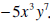 . Its coefficient,
-5, is the
. Its coefficient,
-5, is the
leading coefficient.
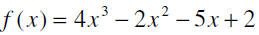
is an example of a polynomial function. In a polynomial
function, the expression that defines the function is a
polynomial.
How do you evaluate a polynomial function? Use
substitution just as you did to evaluate functions in Chapter 2.
EXAMPLE
The polynomial function
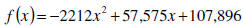
models the cumulative number of deaths from AIDS in the
United States, f (x), x years after 1990. Use this function to
solve the following problem.
Find and interpret f (8).
SOLUTION
To find f (8), we replace each occurrence of x in the function’s
formula with 8.
CONTINUED
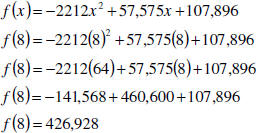 |
Original function |
| Replace each occurrence of x with 8 |
|
| Evaluate exponents | |
| Multiply | |
| Add |
Thus, f (8) = 426,928. According to this model, this means that
8 years after 1990, in 1998, there had been 426,928 cumulative
deaths from AIDS in the United States.
Polynomial functions of degree 2 or higher have graphs
that are smooth and continuous.
By smooth, we mean that the graph contains only
rounded corners with no sharp corners.
By continuous, we mean that the graph has no breaks
and can be drawn without lifting the pencil from the
rectangular coordinate system.
Graphs of Polynomials
EXAMPLE
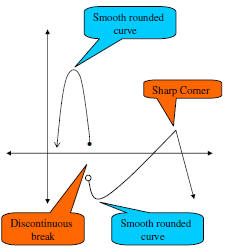
The graph below does not represent
a polynomial function. Although it
has a couple of smooth, rounded
corners, it also has a sharp corner
and a break in the graph. Either one
of these last two features disqualifies
it from being a polynomial function.
| The Leading Coefficient Test | |
| As x increases or decreases without bound, the graph of a polynomial function eventually rises or falls. In particular, | |
| Odd-Degree Polynomials |
If the leading coefficient is positive, the graph
falls to the left and rises to the right. |
| If the leading coefficient is negative, the graph
rises to the left and falls to the right. |
|
| Even-Degree Polynomials |
If the leading coefficient is positive, the graph
rises to the left and to the right. |
| If the leading coefficient is negative, the graph
falls to the left and to the right. |
|
Polynomials
EXAMPLE
The common cold is caused by a rhinovirus. After x days of
invasion by the viral particles, the number of particles in our
bodies, f (x), in billions, can be modeled by the polynomial
function 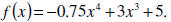
Use the Leading Coefficient Test to determine the graph’s
end
behavior to the right. What does this mean about the number
of viral particles in our bodies over time?
SOLUTION
Since the polynomial function has even degree and has a
negative leading coefficient, the graph falls to the right (and
the left). This means that the viral particles eventually
decrease as the days increase.
Adding Polynomials
EXAMPLE
Add: 
SOLUTION
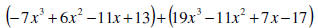 |
|
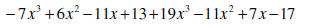 |
Remove parentheses |
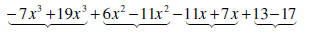 |
Rearrange terms so that like terms are adjacent |
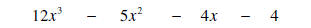 |
Combine like terms |
Subtracting Polynomials
EXAMPLE
Subtract 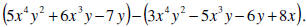
SOLUTION
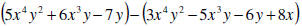 |
|
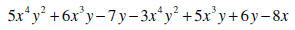 |
Change subtraction to addition and change the sign of every term of the polynomial in parentheses. |
 |
Rearrange terms |
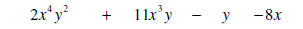 |
Combine like terms |


