Top Algebra Errors Made by Calculus Students

Preface

In recent years, it has been observed that the average student enrolled in an
introductory calculus course at the college level is not as adept as she once was in
her prerequisite algebra/precalculus skills. Whether this comparison with the past
is accurate or not, it is certainly true that the average student makes many errors
of an algebraic (rather than a calculus) nature, and this serves only to divert her
focus from the subject at hand.

To address the issue of poor algebraic skills, many writers of calculus texts now
include a preliminary chapter for the review of precalculus concepts. While, in
theory, such a review seems a good idea, in practice, the benefits, at least in the
opinion of some, are dubious. In the ideal setting such a review would get ample
time (with some students getting advised to take an entire precalculus course at the
college level before entering calculus); instead, it is usually clear that the teacher is
trying to spend the minimal time necessary so as to arrive at the calculus as early
in the semester as possible.

This document was written, both out of experiences that have led to my aban-
doning an algebra review at the start of first semester calculus sections I teach, and
out of certain realities at my institution. As to the former, it is my experience that a
two-week review of precalculus is of little value. One might think that the stronger
students might be bored for a couple of weeks while the struggling ones gratefully
soak in the understanding of precalculus that has previously eluded them. In my
experience, it works the other way around. The strong students | the ones who
would do relatively well with no review | are the most engaged, while the weaker
ones are buoyed up by a false confidence bred out of a sense of familiarity with
the topics. For such students there are two rude awakenings to come at the end of
the review: the score on the exam testing their knowledge of precalculus, and the
very unfamiliar and difficult (to some more than others) concepts of calculus, now
thrown more quickly at them because several weeks were given over to review. It
is a discouraging way to begin a course, and many students never get their heads
above water again during the semester. In addition to experiences such as these, I
have a certain sympathy for the point of view that students who have enrolled in a
calculus course should get just that, not some hybrid course that is inappropriate
both for those who have strong algebra skills, and for those whose lack of algebraic
facility calls for a more extensive study of precalculus.

As to the realities at my institution, recent changes have led to the addition,
rather than elimination, of certain topics which had not formerly been in the first
year of calculus. Roughly speaking, two and a half semesters have been compressed
into two. Many of our students in first-year calculus are studying to be engineers,
and these changes are the result of the attempts on the part of the Mathematics
Department to accomodate the wishes of our Engineering Department, while main-
taining a calculus sequence that is coherent and mathematically sound. As one
might expect, we have tried to make the total course content for both semesters of
calculus comparable to what it was before the change; we have increased breadth at
the expense of depth. Nevertheless, several weeks of review at the start of a course
seems a more remote possibility than before.

It is not my response to ignore the sometimes-incomplete backgrounds of our stu-
dents, but to deal with the issue differently than with an initial precalculus review.
I usually take a just-in-time approach, providing a short treatise on various precal-
culus concepts at the moments they become relevant in our discussion of calculus.
For instance, I usually treat the subject of inverses about the time one discusses the
chain rule, inverse trigonometric functions, or logarithms and exponentials. Still,
the day-to-day algebraic errors which students make, such as the assumption that
all functions behave linearly, are not directly addressed by a review of the most
important precalculus concepts, whether this review comes all-at-once at the begin-
ning of the course, or in short bursts interspersed among calculus topics. It is for
these remaining pervasive errors that I have written this piece.

To be straight about it, its purpose is two-fold. One purpose is as mentioned
above, to provide a detailed discussion of some of the most common algebraic errors.
The other is to reduce the amount of writing a conscientious grader feels compelled
to do. I achieve the latter by giving names and 3 or 4-letter acronyms to the error
types. When one of these errors is seen, a grader need only write the acronym, not
a long discussion of the error. The student who receives the abbreviated 4-letter
comment is not shortchanged in the least. She may turn to this document, look up
the acronym, read the accompanying discussion, and benefit from it just as much
(more?) as she would have from a detailed comment.

Of course, for this grading/commenting system to be successful, students must
have access to this document.

Perhaps the bigger hurdle is that teachers must take the time to read and note
which errors are addressed herein, along with the acronym used for each. It may
take a nontrivial amount of time on the part of the instructor to get accustomed to
all of these. Still, I believe the time invested in the beginning should, in the long
run, reduce an instructor's grading time.

Please address comments on this document | both those intended to improve
discussion of errors already addressed and those indicating an error which you think
should be addressed | to the author. Also, if you use this document, a vote of
confidence by way of a quick email would be appreciated.

Linear Function Behavior (LFB)

Lines through the origin are peculiar in that they have an expression of
the form f(x) = mx, where m is a constant (the slope). This formula
makes possible the following \additive" property:

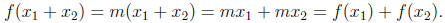
For the particular choices of x₁ = x² and x₂ = 2x, we would have

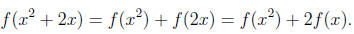
Despite students' tendancies to treat every function as additive, other
functions just do not have this property. Typical mistakes made
include:

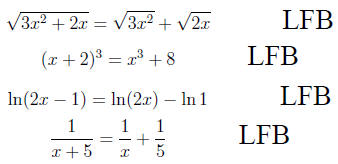
Cancelling Everything in Sight (CES)

Seeing a complicated fraction become less ugly as elements are cancelled
from both the numerator and denominator can be something of an en-
joyable experience. One's first exposure to this magical process usually
comes in grade school when reducing fractions, such as

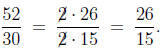
High school algebra classes build upon this, showing us that we may also
cancel expressions involving variables, as in

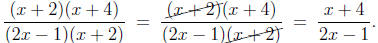
What some students do not notice is that these cancellations only are
performed once the numerator and denominator are factored. Factor-
ing a numerator (or denominator) turns it into an expression which is,

at its top level, held together by multiplication. For instance, in the
expressions

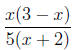	numerator and denominator are factored,
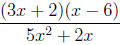	numerator is factored, denominator is not, except as (1)(5x2 + 2x)
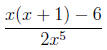	denominator is factored, numerator is not,
	neither numerator nor denominator is factored.

To be sure that one performs valid cancellations only, it is necessary to

•be patient, making sure to factor numerator and denominator first,
and cancelling only those factors common to both, and

•accept that many times no factorization is possible, at least none
that leads to a common, cancellable factor.

With this in mind, cancellations such as those below may only be labelled
instances of someone "cancelling everything in sight", with no attention
given to the discussion above, and having no validity whatsoever.

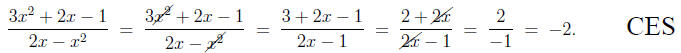
Any attempt to simplify the original fraction (rational expression) should
start with factoring:

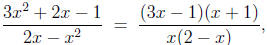
at which stage we see that there is no matching factor between those
of the numerator | namely, (3x - 1) and (x + 1) | and those of the
denominator- (x) and (2 - x). Factoring, in this case, did not lead to
any cancelling, as is often the case.

Confusing Negative and Fractional Exponents (CNFE)

Students can make a variety of mistakes when it comes to working
with exponents. Two of the most common are Multiplying Expo-
nents that should be Added (MEA), and Adding Exponents
that should be Multiplied (AEM). This section does not deal with
either of these, but rather with a problem that some students have ap-
plying two basic rules about exponents, the ones concerning reciprocals
and roots. Specifically, these are

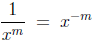and

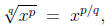
respectively, where the understanding is that a square root ( ) is to
be taken as ( ).

The first of these says that a factor of the denominator (see the
discussion on CES) raised to a power (be it positive or negative) may
be written as a factor to the oppositite power of the numerator (i.e., a
(-2) power becomes (+2), a (3/4) power becomes (-3/4)). The only
change is to the sign of the exponent. An example of a valid application
of this rule is

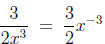or

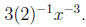
The second rule shows how to write a root as a power, which can be
especially helpful in calculus when a derivative is desired. Things like

	may be written as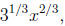
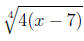	may be written as
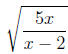	may be written as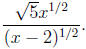

Some students seem to confuse these two rules. The main errors seem
to come from students trying to reciprocate the wrong thing

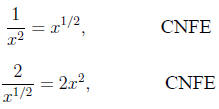
or from students putting a minus in when none is required

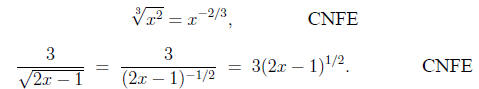
Multiplication Ignoring Powers (MIP)

Another law of exponents frequently misunderstood by students is

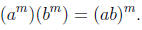
This means that such statements as

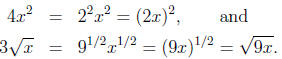
are correct. But many students ignore the significance of having identical
powers in these multiplications. They make statements like the following,
all of which are incorrect:

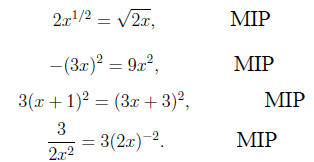
Equation Properties for Expressions (EPE)

Early on in one's high school algebra courses one learns several properties
of equality | namely

•Addition/Subtraction Property of Equality: One may add/subtract
the same quantity to/from both sides of a given equation, and the
solutions of the resulting equation will be the same as those of the
original (given) one.

•Multiplication/Division Property of Equality: One may mul-
tiply/divide both sides of a given equation by the same nonzero
quantity, and the solutions of the resulting equation will be the
same as those of the original (given) one.

Notice that both of these properties pre-suppose that we start with an
equation, usually one we are supposed to solve (say, for x). These prop-
erties are helpful in achieving that goal, as in.
Solve 3x-1 = 7:

Add 1 to both sides: 3x = 8

Divide both sides by 3: x =8/3

or,
Solve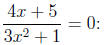

Multiply both sides by the never-zero quantity (3x2 + 1):	4x + 5 = 0
Subtract 5 from both sides:	4x = -5
Divide both sides by 4:	x = -5/4.

In contrast, these are not, generally speaking, properties one uses
when trying to simplify an expression. (There are exceptions to this, such
as in the simplifying of and using integration by
parts, but these are relatively rare.) Students asked to find the derivative
of

may find it easier to work with the function

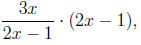or 3x

but they shouldn't be under any illusions that 3x and 3x/(2x - 1) are
the same functions, nor that they have derivatives that are equal. If one
is simplifying an expression like

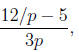
it may be tempting to multiply by p, which gives

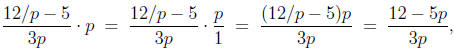
but, of course, multiplying by p changed the expression. One must both
multiply and divide by p (equivalent to saying that we're multiplying by
1) if the expression is going to remain the same (but hopefully simplified):

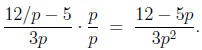
Another example is in simplifying the difference quotient

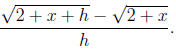
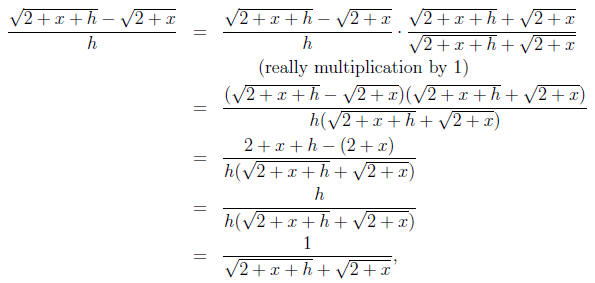
which cannot be further simplified.

Multiplication Without Parentheses (MWP)

The discussion here necessarily must begin with an appeal to the or-
der of algebraic operations (OO). These are rules of hierarchy as to
which operations to perform 1st, 2nd, etc. when an algebraic expression
requires more than one operation be performed. There are three levels
of hierarchy:

(1) powers,

(2) multiplication and division, and

(3) addition and subtraction.

When faced with an expression like the one below that has both an
addition and a multiplication in it, the order of operations dictates that
the multiplication be performed first:

2 + 3 ·5 is 17, not 30.

The levels above do not give the whole story, however. For instance, what
if an expression has both an addition and a subtraction, operations which
appear at the same level? The answer here is that operations appearing
on the same level are always performed left-to-right:

2 + 3 - 5 is 0,

 2 - 3 + 5 is 4,

and 2=3 5 is 10/3
:
Also, one may use parentheses to override these rules. Things in paren-
theses are performed before things outside of those parentheses, starting
from the inside and working out. So

2 - (3 - (2 - 6)) is - 5,

while

2 - (3 - 2 - 6) is 7

and

2 - 3 - 2 - 6 is - 13.

These order of operations apply to expressions involving variables as
well. Thus
 

x· 2x - 7	is not the same as	x(2x - 7),
3 - x/x2		(3 - x)/x2.

In this light, acceptable notation for the product of two expressions like
(3) and (-5x²) is

(3)(-5x²) or, more simply - 15x²,

not, as so many students write,

Frivolous Parentheses (FP)

There really isn't an error, per se, with using too many parentheses.
Nevertheless, students who consistently employ more parentheses than
needed are demonstrating as much of a lack of understanding of the order
of algebraic operations as those who use too few. Expressions such as

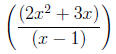	look simpler as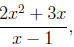
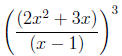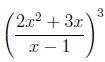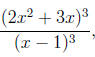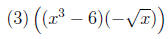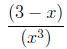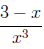	or
	or

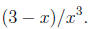Undo Multiplication with Division (UMD); also, Undo Addition with Sub-
traction (UAS)

The properties of equality that were mentioned earlier are, by some
students, implemented incorrectly even when the situation calls for their
use. For instance, when solving an equation like

3x + 7 = 4,

two steps are called for:

3x = -3 (subtraction prop. of equality; 7 subtracted from both sides)

and

x = -1 (division prop. of equality; both sides divided by 3):

Notice that, in the expression (3x + 7), the order of operations dictates
that the multiplication by 3 comes before the addition of 7, and the
"undoings" of these processes | the subtraction of 7 and the division
by 3 | were carried out in reverse order. That is not to say that we had
to undo things in this order, but students who use a different sequence
often make the following error. Dividing by 3, they often neglect the
fact that all terms on both sides are to be divided by 3. In other words,
after dividing by 3 they write

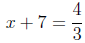instead of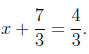

They are too set on the idea that they will be subtracting 7 from both
sides to realize that, having divided by 3 first, it is not 7, but rather 7/3,
which must be subtracted, giving the same answer x = -1 as before.
One other note is in order here. If parentheses appear in an equation
such as

3(x - 1) = 5,

then the order of operations are preempted (the subtraction within the
parentheses comes before the multiplication by 3). In solving for x, we
may of course, distribute the 3, thereby eliminating the parentheses and
making the problem appear similar to the last one discussed. Even fewer
steps are required if one just \undoes" the multiplication and subtraction
in their opposite order:

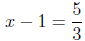(division prop. of equality; dividing both sides by 3);

and then

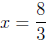(addition prop. of equality; adding 1 to both sides).

Now let us return to the equation

3x + 7 = 4,

and investigate the more telling errors that gave the titles UMD and
UAS to this section. Some students recognize the need for two steps
(like those carried out when this equation was being considered above)
to isolate x, but have little feel for which operations will achieve this. For
instance, realizing that, like the 4 on the right-hand side of the equation,
7 is a "non-x" term, a student may write

misunderstanding that she has subtracted 7 on the left side, but divided
by 7 on the other side. The original equation and the new one no longer
have the same solution as a result. The same student may then recognize
that she needs to move the 3 over to the other side. Since the 3 is
multiplied by the x, she should \undo" this by dividing both sides by 3.
But she may (wrongly) write

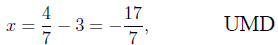
having divided on the left but subtracted on the right. Again, the so-
lution (x = -17/7) is different from the one that solved the original
equation 3x + 7 = 4, namely x = -1.

Worse still is when a student thinks he can solve in one step (that is,
take care both of the multiplication by 3 and the addition of 7 via one
operation). Such a student may write something like

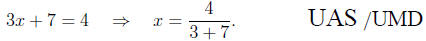
Again, the answer this student gets, x = 2/5 , is different than the correct
one x =-1.

Misunderstood Relationship between Roots and Zeros (MRRZ)

Much of one's mathematical experience prior to the calculus is spent in
solving equations. There are the kind of equations, known as identities,
where every number in the domain is a solution. The equation

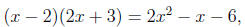
is such an identity. It is not this, but the other type of equation, known
as a conditional equality, that one learns to solve, precisely because so-
lutions, also known as roots, of conditional equalities are not everywhere
to be found. Often there are very few numbers, perhaps even none at
all, which make a conditional equality true.

Another fact about conditional equalities is that comparatively few of
them may be solved exactly. Leaps in technology have made it common-
place for students, with the purchase of a handheld calculator, to have at
their fingertips powerful graphing capability and numerical methods for
finding approximate solutions to many, perhaps even most conditional
equalities. This does not mean that one should forego learning the al-
gebraic techniques which lead to exact solutions, thinking that deftness
in pushing the right pair of buttons is an appropriate substitute for the
thought processes such algebraic methods introduce. Still, there is added
value in the knowledge one gets by investigating graphical methods. By
these methods one comes to think of the solutions of, say,

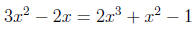
as the x-values of points of intersection between the graphs of the two
functions

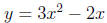and

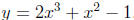
As another example, solutions of the equation

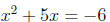
would be found at points of intersection between the graphs of

y = x² + 5x (a parabola) and y = -6 (a horizontal line),
It is in solving equations like this latter one that students become con-
fused. What some students do is the following:

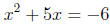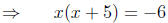	(factor the left side)
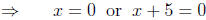	(set factors equal to zero)

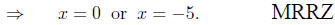In mathematical terms, the student who does these steps has found the
zeros of f(x) = x² + 5x; that is, the values for x which make the output
of f be zero. There are several ways to see that this work is wrong. One
way to see it is that, in the equation, we want values of x whose output
value is (-6), not zero. Another angle which reveals the errors is the
one that notes that, while there are a lot of pairs of numbers which may
be multiplied to give (-6) - (-1) and 6, 12 and (-1/2), 55 and (-6/55)
are three such pairs - one thing which we can say for certain is that
neither of the numbers in the pair is zero, which is quite counter to the
idea of setting the factors equal to zero. (Of course, neither is it enough
to set the factors equal to (-6), as in

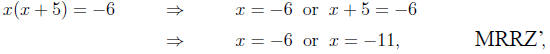
since it is not enough for either one of these conditions to hold by itself;
that is, if x = -6 then we would need the other factor (x + 5) to be
equal to 1 in order for their product to be (-6), and clearly these things
cannot occur at the same time.)

In summary, the error occurs in finding the zeros of a function and
taking them to be the roots of the equation, when the two concepts do
not coincide. There is a simple way to make them coincide. We simply
make one side zero (using a valid algebraic step, of course).

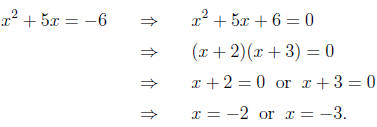
The zeros of g(x) = x² + 5x + 6 are the numbers which make g equal
zero, and that is exactly what we want in a solution of the equation
x² + 5x + 6 = 0, so the two concepts coincide. Why do students mess
this up? The most likely answer is that many are looking to do as
little work as possible, and bringing the (6) over makes factoring a more
difficult job (it is harder to factor x² +5x+6 than to factor x² +5x); of
course, the quadratic formula is an option for this case. What may help
to avoid this confusion is remembering this graphical interpretation of
what one is doing (still applied to the example above):

•Solutions of an equation like x² + 5x = -6 correspond to points of
intersection between the two sides, considered as functions, of the
equation (i.e., the function x² + 5x and the function, in this case a
constant one, (-6)).

•If the two functions are combined into one function on one side of
the equation, there is still a second function, the zero function, that
remains on the other side. Now we have in place of the old problem
a new one (but entirely equivalent) of finding the solutions that
correspond to points of intersection between the new left-hand side
(in this case x² + 5x + 6) and the new right-hand side (here zero).
When our combining of terms has left one side of the equation zero
(which, when considered as a function, has the x-axis as its graph),
one may solve the equation by finding the zeros of the other side of
the equation.

Multiplication Not Distributive (MND)

In precalculus/algebra we become familiar with the distributive laws that
address interactions between multiplication and addition/subtraction.
Specifically, these laws say

a(b + c) = ab + ac and (a + b)c = ac + bc.

We use these laws all the time, both in expanding

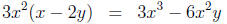and

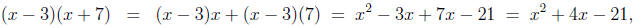
and in factoring

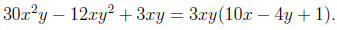
We even use it (although we don't often think about it this way and
usually don't include the middle step below) when combining like terms,
as in

The problem is when students misinterpret these laws, thinking they also
say something about interactions between more than one multiplication;
that is, they "invent" for themselves a law that looks something like:

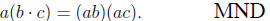
This clearly is false, as most would see if these were all numbers | few
(though I cannot go so far as to say no one) would assert, say, that

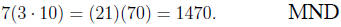
But when the objects involved are expressions involving variables, the
error is frequently made, such as in this case:

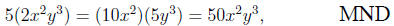
or

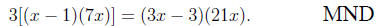
Poor Use of Mathematical Language (PUML)

A prerequisite skill to writing good mathematics is the ability to write
well in one's native tongue. People who cannot write a complete English
sentence should take remediation in English composition before reading
on.

What may surprise some students is that good writing using math-
ematical symbols (even in the write-up of homework problems) consists
of using complete sentences, setting up one's ideas clearly and then fol-
lowing through on the details, much as one expects from a good English
essay. The language and symbols of mathematics are used just like reg-
ular English words and phrases to express ideas, albeit ideas which one
would often struggle to use any other means of expressing.

Nobody studies mathematical writing as a subject. Your mathemat-
ics professor(s) got to be good writers of mathematics, if good they be,
by the reading papers and books of other mathematicians, not by read-
ing a treatise such as this one. If a book on good mathematical writing
does exist (and there probably are a number of such books), they will say
much more than I say here. I will only describe the most common ex-
ample of poor mathematical writing I see when grading students' work:
Using Equals as a Conjunction (UEC).

The word \equals" has a very specific meaning. It requires two ob-
jects, and it asserts that these two objects are the same. In mathematics,
the two objects are usually quantities, like the mathematical expression
(3x + 5), or the number 7. Even within this tight definition, mathemat-
ical equations, as I mentioned earlier, come in two varieties: identities
and conditional equations. A conditional equation is one such as the
equation

3x + 5 = 7;

which is true only for particular values of x (in this case one particular
value). In algebra courses one often sees conditional equalities in home-
work problems accompanied by the instruction "Solve the equation".
There are some quantities that are the same regardless of the value of
the variable. A familiar example is the identity

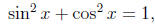
which is true no matter what real value x takes. These two types of
equations encompass the two most common (and only?) valid ways to
use an `equals' (=) sign.

Consider the typical calculus problem of evaluating a limit like

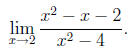
What we are given here is not an equation, but an expression. If we
begin writing a series of equalities to simplify/evaluate this expression,
we will want them to be identities, as in

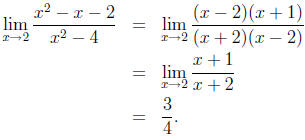
The original expression, along with each of the ensuing expressions, as
it turns out, are all equal to the number 3/4.

In contrast, suppose we begin with a (conditional) equation like

3x + 5 = 7,

which we are asked to solve. If a student who understands very well
the discussion of UAS and UMD (found earlier in this piece) makes a
mistake, she is most likely to do so writing something like

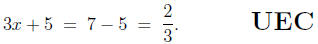
Such a string of equalities asserts three things:

Such a string of equalities asserts three things:

(i) that 3x + 5 = 2,
(ii) that 3x + 5 = 2/3,
(iii) and that 2 = 2/3.

(i) and (ii) are conditional equations in their own right, but it should be
clear that they do not have the same solutions as the original equation
3x+5 = 7 (nor does (i) have the same solution as (ii)). And (iii) has no
solution at all, for it is never true. What I am really saying is that the
string of equations

is really three equations, and there is no common solution between them
(and, even if there had been, such a solution would have no relevance to
the original problem, that of solving 3x+5 = 7). The student most likely
never intended to assert these three equations in place of the original; she
simply began writing out her ideas, and used an equals sign to join them
together whenever it seemed some sort of `conjunction' was required.

The student who writes (1) actually appears to have some facility in
the techniques for solving linear equations, but lacks the ability to put
her ideas onto paper in a meaningful fashion. One good way to express
the solution of the previous equation is

The symbol=> can be translated here as \which implies". Yes, (2) is
more writing than (1), much in the same way the complete sentence "I
am taking the train to Chicago this weekend" requires more writing than
the three words \weekend, Chicago, train". A more favorable comparison
is between (2) and the same ideas expressed in English words:

If the sum of three times x and five is seven, then subtracting
five from both sides and dividing by three yields the value of
two-thirds for x,

or, perhaps more literally,

Assuming that the sum of three times x and five is seven, this
implies that three times x is two, and that x is two-thirds.