Factoring Polynomials with Common Factors
Section 6.4 Slope and Graphs of Linear Equations
Read section 6.4, pages 347 - 352 and answer the following questions as you
read:
1. Make a note card for the difference of two squares. On the card,
explain, in words, how you recognize an expression in this form.
2. Circle each of the following expressions that are a difference of two
squares, then factor them. If it is not the difference of two squares,
explain how you know.
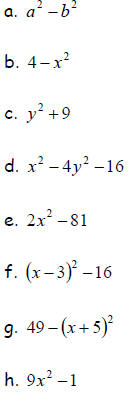
3. Make a note card for perfect square trinomial. On the
card explain in
words how you recognize an expression in this form. Explain how the
middle term is related to the first and third terms. Which terms must
always be positive? Why?
4. Find two values of b in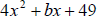 
such that the
expression is a
perfect square trinomial.
5. Identify each of the following expressions that are a
perfect square
trinomial. Factor each perfect square trinomial. Otherwise, explain
how you know it is not a perfect square trinomial.
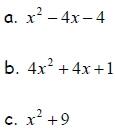
6. Make a note card for sum and difference of two cubes.
On the card,
explain, in words, how you recognize expressions in these forms.
6. For each of the following, write an example, then factor it, if possible.
| a. difference of two squares | |
| b. perfect square trinomial | |
| c. sum of two squares (NOT FACTORABLE) |
|
| d. sum of two cubes | |
| e. difference of two cubes |
Section 6.5 Equations of Lines
Read section 6.5, pages 356 -362 and answer the following questions as you
read:
1. If we multiply two numbers and the result is 0, what do we know about
the numbers?
2. a. If (x - 3)(x + 4) = 0, what can you say?
b. If x(5 – x) = 0, what can you say?
c. If (x + 2)(x – 6) = 8, what can you say?
3. Which of the following are quadratic equations? If it is not, explain
how you know.
4. What is the general strategy for solving quadratic
equations?
5. What is the general form of a quadratic equation?
6. For each of the equations, explain what you would you
do first to solve
it.
7. Solve each of the equations in #6.
8. Study example #7 to solve this similar problem.
The product of two consecutive positive integers is 42. What are the
integers?
Verbal model:
Labels:
Equation:
Solve it:
Write your answer in a complete sentence:
9. Study example #8 to solve this similar problem.
A ball is dropped from the top of a building 64 feet high.
The height
(in feet) of the ball is modeled by the equation
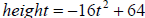where t is time measured in seconds.
a. What is the height of the ball after 1 second?
b. How long will it take the ball to hit the ground?
10. Study Example #9 to solve the problem:
A rectangular great room (family and dining areas) has an area of 480
feet. The width of the room is 4 feet less than the length. Find the
dimensions of the room.
Verbal Model:
Labels:
Equation:
Solve the equation:
Write your answer in a complete sentence:
Review of Chapter 6
Finish filling in the steps of the flow chart to help you make decisions about
how to factor all polynomials in this chapter.
