Sample Math Problems

1. Suppose we are given real numbers w, x, y, and z such that x < y and w < z.
Determine if each of the following inequalities is true or false or inconclusive (i.e., it
could be either true or false).

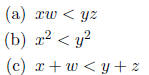
Solution:

(a) Let us look at some examples: If we take numbers greater than 0 then the
inequality seems to hold. For example,

x = 3 < 4 = y
w = 2 < 7 = z
xw = 6 < 28 = yz

However, if we take numbers less than 0, then the inequality does not hold. For
example take

x = −3 < −1 = y
w = −4 < −2 = z.
But
xw = 12 > 2 = yz.

So this inequality one may or may not be true, depending on the real numbers
chosen.

(b) This inequality will again depend on the numbers chosen. To see this, let us
again choose numbers that are greater than 0 and then numbers that are less
than 0. It is clearly true that x = 3 < 4 = y and x^2 = 9 < 16 = y^2, but if we
take x = −4 < −3 = y then x^2 = 16 > 9 = y^2.

(c) Again, let us choose specific numbers, say, −3, −2, 0, and 5. We have that
−3 < 5 and −2 < 0. It is clear that −3 + (−2) < 0 + 5. The fact is that the
inequality is always true, given the conditions.

How shall we prove it? From x < y we can say y = x + p with p > 0. From
w < z we can say that z = w + q with q > 0. So

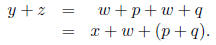
Thus y + z is x + w plus (p + q). Note that (p + q) is positive since each of p, q
is positive. So we get x +w < y + z.

(d) Summary. How do we decide to prove or disprove the inequality? In general,
remember that multiplication by negative numbers reverses an inequality, so
whenever products are involved, we suspect failure.
When only additions or multiplications by known positives are involved, we expect
the inequality to be true, provided the algebraic manipulations can show its
truth.
In general, proving the inequality true involves general calculations, whereas
proving it to be false or inconclusive is done by a simple example!
Even though our examples are fairly simple, in real life, inequalities can be lot
more complicated than equations.

2. Let f(x) = x^3 + x + 2 and g(x) = 3x^2 + x. We will find deg_x(fg).

Solution:

One approach would be to multiply the polynomials term by term and note the degree.
But this is not necessary. Let us recall the the product rule for degrees. The degree
of the product of two non-zero polynomials is the sum of their degrees. Therefore

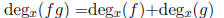
We note that deg_x(f) = 3 and deg_x(g) = 2. And so deg_x(fg) = 3+2 = 5.
From experience you could also say

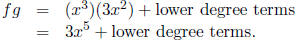
Thus we even know the highest degree term!

3. Let us define s to be the monomial Find the coefficient of s in general as well
as the coefficient of s when it is regarded as a monomial in x or y.

Solution:

• To begin, it is good to simplify s to the expression
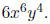
• Now simply note that for s = 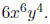the coefficient is 6 and the degree is the
sum of the powers of the variables, i.e., 6 + 4 = 10.
• If we regard s as a monomial in x then let we rewrite it as As a monomial
in x its coefficient is 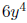and the degree is simply 6.

• Finally, let us regard s as a monomial in y and rewrite it as So, as a
monomial in y, the coefficient is 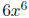and the degree is 4.

4. Let and Find the coefficient of x
in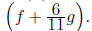

Solution:

One approach would be to find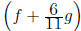explicitly.

A simpler approach is to recognize that since we are adding polynomials, the only
terms that contribute to the coefficient of x in are those coefficients of x
in f and g. In f we have 12x and in g we have −11x. Then the term with x in
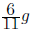
is
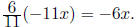
So the term with x in is

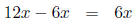
The desired coefficient is then 6.
A better strategy would be to do a more general problem and avoid numerical errors.
Consider the more advanced problem:
Find the coefficient of x in af + bg where a, b are constants. Clearly the x-term in
af + bg will be

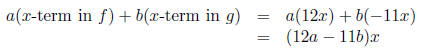
Thus the desired coefficient is 12a−11b. For the given problem we have a = 1, b =
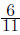
so the answer is 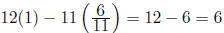as before.

5. Let 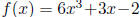and Find

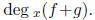
Solution:

We can, of course add the two polynomials, collect the coefficients and then find the
degree.
But that might be more work than needed.
Recall the facts:

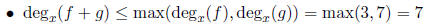
• Also the coefficients of x⁷ in f, g are respectively 0, 1. So the coefficient of x⁷ in
f + g is exactly 0 + 1 = 1.
• The above two facts tell us that we must have:

lower degree terms .

Hence the desired degree of f + g is exactly 7.

• To remember: We may remember once for all that the degree of a sum f + g
is equal to the maximum of the degrees of f and g as long as the two degrees
are distinct! When the degrees of f, g are equal, then the answer depends on
the cancellation of terms and any degree less than or equal to the maximum is
possible, including the chance that f + g may be zero!

6. Use Cramer’s rule to find the solution to a system of two equations in two variables:

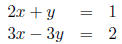
Solution:
Calculate

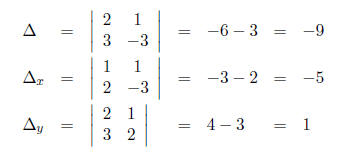
So

Recommendation:
It is an excellent idea to double check your answer. Plug the answers in each of the
equations and verify that they are true:

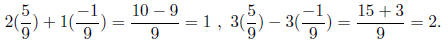
7. Solve a system of two equations with two variables using substitution.

Solve:

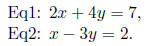
Solution:
Solving Eq2 for x gives
Solution1

x = 2+3y.

Plugging this into Eq1 gives

Now we use this value for y in Solution 1,

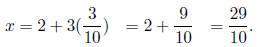
So the final solution is

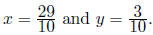
As before, we recommend that you double check the answers. Either use Cramer’s
Rule or substitute the answer and verify each equation.

Check:

Eq1:

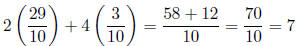
Eq2:

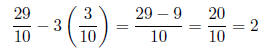
8. Let f(x) = 2x^2 −3x+4. Find the equation for the line tangent to y = f(x) at x = 2.

Solution:

To write the equation of any line, it is enough to know a point on it and its slope.

To find the point we simply note that x = 2, y = f(2) is on the line.
For the slope of the line, we know that the slope of a tangent line is given by the
derivative of f(x) at x = 2, i.e. f'(2).

• Let us evaluate f(2).

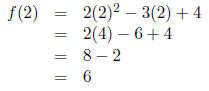
So the point is (2, 6).
• Next, let us find f'(x) in general. By the power rule,

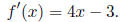
So f'(2) = 4(2) − 3 = 5 and the slope of the tangent line at (2, 6) is 5.
• Using the point slope formula, (y − y₁) = m(x − x₁) where m = 5, x₁ = 2, and
y₁ = 6, we see that the equation for the tangent line is

(y − 6) = 5(x − 2), or y = 5x − 4.

There is an alternate technique based on theory. We consider the equation y =
2x^2 −3x+4 and to find the tangent at x = 2, y = f(2) = 6 we rewrite x = 2+u and
y = 6+u.Substitute this in the given equation and keep only the linear terms.

Thus y = f(x) becomes

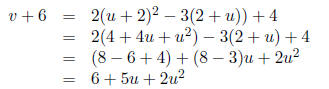
Thus the linear part becomes
u = 5u
or
(y − 6) = 5(x − 2)
This is the desired tangent line!

Let A(2, 7) and B(4, 5) be points in the plane. Find an equation of the line passing
through A and B and put it in slope-intercept form.

Solution:

(a) First, we find the slope of the line by using the slope formula. Recall that the
slope of the line joining P₁(a₁, b₁), P₂(a₂, b₂) is given by the formula

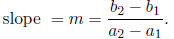
Using P₁ = (2, 7) and P₂ = (4, 5) we get:

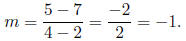
So the slope of the line is −1.
(b) Now, we choose a point, say, P₁(2, 7) and use the point-slope formula.

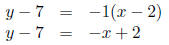
Rearranging:

y = −x + 9

(c) Thus the slope is −1 and y-intercept is 9.
(d) Short cut! Recall the two point formula from the book (for same points P₁, P₂
as above):

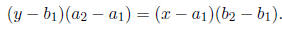
Using P₁ = (2, 7) and P₂ = (4, 5), we get:

(y − 7)(4 − 2) = (x − 2)(5 − 7)

or when simplified:

2y − 14 = −2x + 4	which further becomes
2y = −2x + 18	or
y = −x + 9.

10. Given the points P(2, 3) and Q(5,−1) find the equation of the line passing through
these points in both standard and parametric form.

Solution:

(a) To find the standard form we find the slope, m, and use the point-slope form of
a line. Recall that 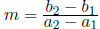and the point slope form is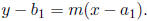

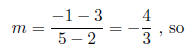
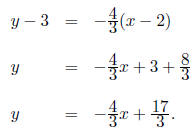
(b) To find the parametric form, recall that possible equations for parametric form
are 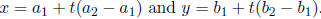So we have

x = 2+t(5 − 2) = 2 + 3t , and
y = 3+t(−1 − 3) = 3 − 4t.

Note that if we eliminate t from these we get
4x + 3y = 4(2+3t) + 3(3 − 6t) = 8+9 = 17.

Which also leads to
3y = −6x + 17
or

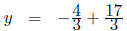
11. Given a line 2x+4y−7 = 0 and a line given parametrically by x = 3t+3 and y = t−2,
determine where they intersect.

Solution:

First, plug in the parametric values for x and y from the second line into the equation
of the first to determine the t value at the point of intersection.

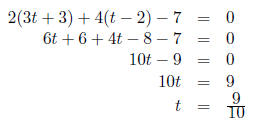
Now find the x and y values for

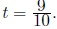
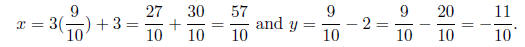
Checking:

12. Convert the parametrically given line, x = −t+2 and y = 2t−1, into standard from,
y = mx + c.

Solution :

We wish to eliminate t from the parametric equations

x = −t + 2
y = 2t − 1.

If we multiply the first equation by 2, the second by 1 and add them together we get:

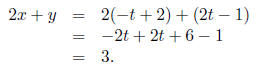
Thus 2x + y = 3 is an equation of the line. In slope-intercept form it becomes
y = −2x + 3.

13. Find the point where the line y = −2x and the circle x^2 + y^2 = 20 intersect.

Solution:

Since the equation for the line is already solved for y we simply plug the value for y
into the equation for the circle:

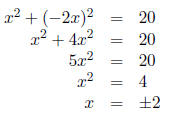
Thus the line intersects the circle at the x-coordinates x = 2 and x = −2. The
corresponding y-coordinates come by using y = −2x. Thus y = −4, 4 respectively.
The two points, respectively, are (2,−4), (−2, 4).