Row Reduction
Row reduction is a method which greatly simplifies taking
the
determinant. (It is also used when finding the inverse or diagonalizing a
matrix.) Rows are the across lines in a matrix. We can write matrices in a
variety of ways. One is just to write it as it is with i’s standing for row
number and j’s standing for column number; another is to write it with one
symbol; or, as we wish to do right now, in terms of all its rows. In these
symbols,
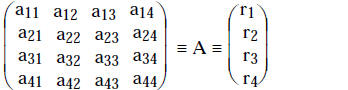 (
1 )
(
1 )
This notation generalizes to an n-dimensional matrix.
There are three useful
elementary row operations that can be performed on matrices.
| Here are the row operations... | ...and how they affect determinants. |
| (1) switch two adjacent rows ri and ri+1. |
(1) makes the determinant switch sign. |
| (2) multiply a row ri by a scalar m to obtain a new row µri. |
(2) multiplies the determinant by µ. |
| (3) replace a row ri with a sum of itself and the multiple of another row, i.e. ri + µrj |
(3) no effect on the determinant. |
(If you think about it, anything linear you can do to a
row is a form of one
of these.)
(1) Why? This has to do with deep facts about determinants that very few
people ever want to know. See an advanced linear algebra text.
(2) Effectively this means that when you multiply the row by µ you
compensate by putting a 1/µ outside the determinant.
 ( 2 )
( 2 )
This kind of makes sense as you are multiplying by one thing and dividing by
the same thing to cancel the effect it has on the determinant.
(3) To see why adding two rows won’t affect your determinant, try an
example or two.
The point of all of this is that rules (1) - (3) allow you to take an ordinary,
unsuspecting matrix and turn it into an upper triangular matrix without
changing the value of its determinant. Once you have that, you can simply
multiply along the diagonal to get your determinant.
You might have thought that you would have to have a matrix with only
entries on the diagonal to calculate determinants so simply. However, if you
consider the operations you wneed to employ to eliminate the elements
above the diagonal they would all be of the elementary row operation type (3),
which doesn’t affect the determinant.
For an example follow the first 4 steps of the reduction of the matrix on
the next page. Stopping at that point gives a determinant of -18, which may
be check by direct calculation.
Row reduction is easy to implement on the computer and this therefore
frequently used for handling various matrix operations.
Inverting Matrices: The inverse of a matrix is one such that if you multiply a
matrix by its inverse, you obtain the identity matrix. The inverse of matrix M
is denoted M-1. If you were trying to invert a matrix rather than trying to take
its determinant, you would place the identity matrix next to your matrix and
perform the same type of row operations as you would to take a determinant.
However, you would perform them on the identity matrix as well (which
would of course cease fairly quickly to be the identity matrix). The quirk here
is that in this process you can’t just stop when you have an upper triangular
matrix; you have to take the original matrix completely to the identity,
because this (using the parallel stuff on the identity matrix) will give you the
original matrix’s inverse, from the identity.
Here's an example:
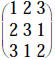 |
(matrix M) |
 |
(start with identity matrix on right) |
 |
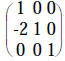 |
op #3 using 1st row on 3rd row of both |
|
 |
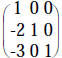 |
op #3
using 1st row on 3rd row of both |
|
 |
 |
(op #2 twice; mult. rows 2 & 3 by -1) (effect on determinant cancels) |
|
 |
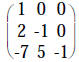 |
op #3 using 2nd row on 3rd row of both |
(At this point it is trivial to evaluate the determinant of M. None of our
elementary row operations changed the determinant so the determinant of
the left-hand matrix immediately above is the same as that of M. Only one
diagonal row contributes and therefore det(M) = -18. This can be checked
from the original form of M. det(M) = 1 x 3 x 2 + 2 x 1 x 3 + 3 x 2 x 1 - 3 x 3
x 3 -
1 x 1 x 1 - 2 x 2 x 2 = 6 + 6 + 6 - 27 - 1 - 8 = -18. √) Now we continue with
finding M-1.
 |
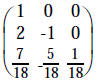 |
(divide 3rd row by -18) |
 |
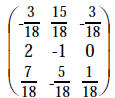 |
op #3 using 3rd row on 1st row of both |
 |
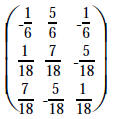 |
op #3 using 3rd row on 2nd row of both |
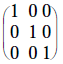 |
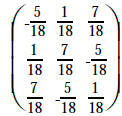 |
op #3 using 2nd row on 1st row of both . |
So 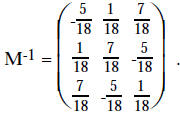 We can check this as follows.
We can check this as follows.
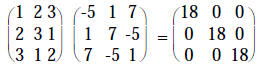
So, it works!


