Addition, Subtraction of Radical expressions

Sections 8.4: Addition, Subtraction of Radical expressions

A. Simplify Completely:

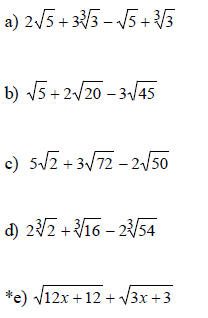
B. Simplify (page 473 in the book)::

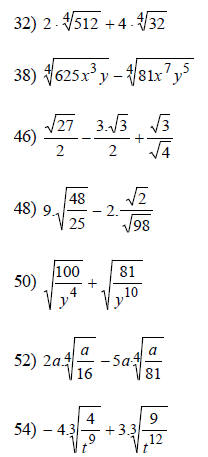
Sections 8.5: Multiplying and Dividing of Radical expressions

A. Multiply and Simplify Completely

B. Multiply and Simplify Completely, (apply (a -b)(a +b) = a^2 - b^2 when it is possible):

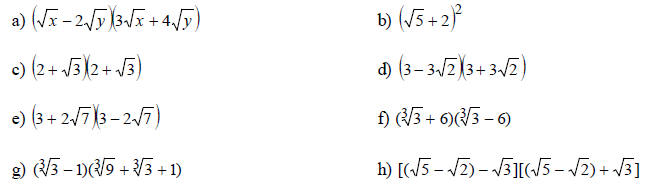
Rationalizing the Denominator: Remove the radical from the denominator

· To remove square root, multiply numerator and denominator by the same square root.
Example:

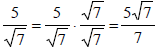
· To remove roots that are not square, follow the following examples and see what is needed to be done to
remove the roots:

If the denominator is:	Multiply Num and Den by:	Result

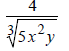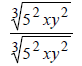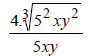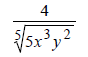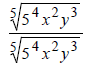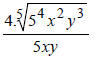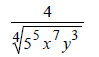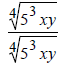You multiply by a root with Same Degree, and make the power of each element under the new root equal to a
number that can be added to the original power (of the same element). The result should be a number that can be
divided by the degree of the root.

For example ,if the degree of the root is 4 and if the power of x under the original root is 7, then the power of x
under the new root should 1 because 7 + 1 = 8 which can be divided by 4.

C. Rationalize :

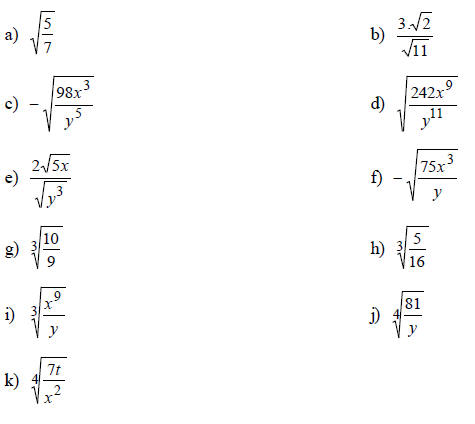
Rationalizing Binomial Denominator

Using: (a - b)(a +b) = a^2 - b^2

D. Rationalize :

E. Write each expression in lowest terms. (page 483 in the book):

F. Rationalize (page 483 in the book):

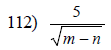
Sections 8.6: Solving Equations with Radicals

A. Solve for x (check your answers):

B. Solve for x (check your answers):

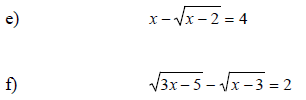
step 1) isolate one radical on one side
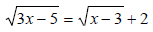
step 2) square both sides, this will remove the radical that was isolated on one side.

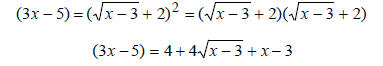
step 3) isolate one radical on one side
step 4) square both sides and simplify: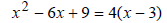
step 5) find the answers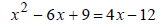
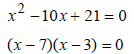	The answer: x = 7 or x = 3.

step 6) check the answers

C. More Examples, solve for x:

D. Rewrite the expression with radical exponents as radical expression and then solve. (page 492 in the book):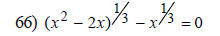

E. Rewrite Solve for the indicated variable. (page 492 in the book):

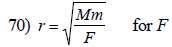
Sections 8.7: The Complex Number

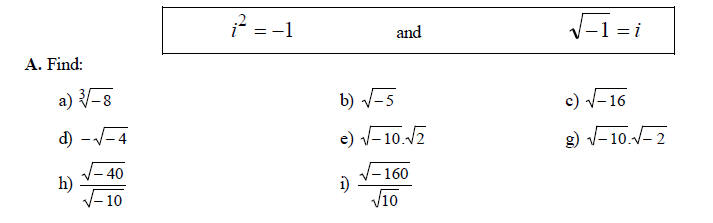
Complex Number is any number in the form a + bi

B. Add and subtract and write your answers in the form a + bi:
a) (9 + i) - (3 + 2i)
b) (-1+ i) + (2 + 5i) + (3 + 2i)

C. Multiply:
a) (2i)(3i)
b) -2i(3 + 2i)
c) (1 + 2i)(2 - 3i)
d) 3i(- 3 - i)^2

D. Multiply using the property of (a - b)(a +b) = a^2 - b^2
a) (2 + 3i)(2 - 3i)
b) (2 + i)(2 - i)
c) (5 + 2i)(5 - 2i)
d) (7 + 2i)(7 - 2i)

E. Divide and write the answer in the form a + bi

F. Simplify using the principle of i^2 = -1: