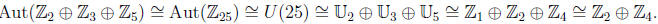Solution to some problems in Math 301 Chapter 11
2) We can just try successive values of n. We can skip
prime numbers as they have only
one isomorphism type (cyclic groups).
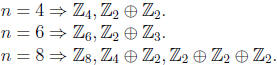
We used here Theorem 11.1 and Theorem 8.2 (especially Corollary 2 for the
latter).
Hence the answer is n = 8.
6) 
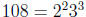. Any decomposition
corresponds to a factor of
or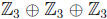 
, and these give at least two subgroups of
order 3, taken from each
factor, with the identity element put in the other factors. So to get one
subgroup
exactly of order 3, the 33 = 27 should not be decomposed as
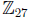has a unique
such
subgroup < 9 >. Hence the two groups are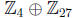 
and
.
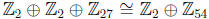Clearly the other factor in these cases has no such subgroup, and as 3 is prime,
one
cannot get a subgroup of this order by combining other nontrivial subgroups of
the
two factors. Hence these are two Abelian group satisfying the required
condition.
12) Corollary 1 to the Fundamental Theorem 11.1 shows that lGl has a subgroup H
of
order 10. As it is a subgroup of a finite Abelian group, H is finite Abelian.
But the
unique isomorphism type of this subgroup is, by Theorem 11.1, just
.
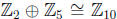the last isomorphism by Corollary 2 to Theorem 8.2. And the latter is a cyclic
group.
20) If G does not have prime power order, then at least two prime powers in the
prime
factorization of lGl have a common factor k (Theorem 8.2 and corollaries). This
factor
is of course also a divisor of G. But then both cyclic groups corresponding to
the prime
powers via Theorem 11.1 have a subgr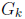oup 
of order k, so by choosing this
subgroup
in one of the two factors and the identity everywhere else (e.g.
one
gets a subgroup of order k in G, and since this can be done for both prime
powers, one
gets two distinct subgroups of order k, contrary to the assumption.
Hence we may assume that G is isomorphic to a group of prime power order. Take
an element x in G of maximal order, say pl. Any element y in G has order lyl
which
divides lxl = l < x > l, so it is pl, 0 ≤ r ≤ l. But this means that, as < x >
is cyclic,
it has a subgroup of order pr = lyl. But we assume there is only one such
subgroup
in all of G, and < y > is such a subgroup. Therefore, < y > must be a subgroup
of
< x >. But this holds for y in G, which means that all of G is a subgroup of < x
>,
while also < x > is a subgroup of G. Hence G =< x >, so G is cyclic.
32) This problem uses the result of Problem 11 in this chapter. Write
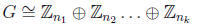
with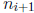 
dividing 
. In our argument we will
identify the left hand side with the
right hand side. An element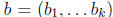
has maximal order
.
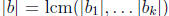Now each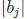 
j divides
(Lagrange for cyclic groups), and each
divides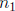 
.
So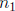
is a common multiple of the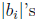 
, so
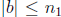. But a = (1, 0, 0... 0) is an element of
order
. Hence a is an element of maximal
order, equal to 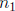, and any b in G has order lbl which divides
.
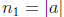36) If two groups G and H are isomorphic, so are their automorphism groups (the
map
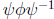, where Ø is an automorphism of G and
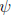. G → H is an isomorphism, gives a
corresponding automorphism of H). So by Corollary 2 to Theorem 8.2, Theorem 8.3
and its corollary and Theorem 6.5,
