Linear Systems I
Outline
What is a linear system?
Examples of systems arising in applications
Systems of equations
A general category of numerical problem is systems of
equations in
which we have m statements about n variables x1, . . . , xn:
y1 = f1(x1, . . . , xn)
y2 = f2(x1, . . . , xn)
...
ym = fm(x1, . . . , xn)
The fs are known functions, the ys are given quantities,
and the xs
are the unknown variables to be determined.
Linear functions
A function f is linear if
f(x + x') = f(x) + f(x')
and
f(ax) = af(x)
for any a, x and x'.
If f is a function of one variable, it has to be f(x) = ax for some a.
If f is a function of n variables it has the form
f(x1, . . . , xn) = a1x1 + a2x2 + · · · + anxn.
Systems of linear equations
A linear system is just a system of equations
yi = fi(x1, . . . , xn)
where the functions fi that define it are linear. This means a system
of m linear equations in n variables looks like this:
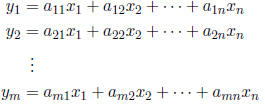
(I have switched to the convention for linear systems that the un-
knowns go on the right.)
Matrix form of linear system
A linear system can be written as one equation using matrix notation.
A small example:
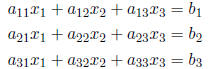
becomes
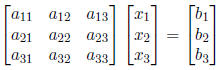
Ax = b
For those who enjoy dots:
Ax = b
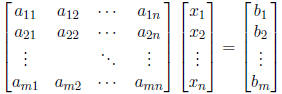
A system of m equations in n unknowns is an equality with an
m-vector on one side and the product of an m × n matrix with an
n-vector on the other side.
Geometric transformations
Suppose we have a coordinate system transformation:
x' = ax + by
y' = cx + dy
and we want to nd the (x, y) that goes to (x', y'). This is a 2 × 2
linear system.
Circuit analysis
Here is a simple circuit:
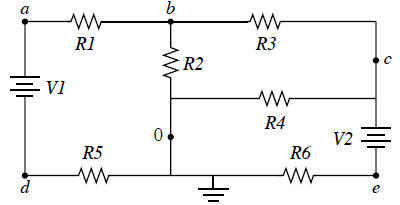
What are the voltages across all the components? A straightforward
analysis but tedious on paper.
• Variables
◦
voltages at nodes: va, . . . , ve
◦
currents through voltage sources I1, I2
• Equations
◦
net current at each node is zero
◦
known voltages across voltage sources
Result is a system with 7 variables and 7 equations
Radiative transfer
Problem in heat transfer: equilibrium energy distribution.
In, for example, a furnace, surfaces exchange heat by thermal
radiation.
• Each surface emits radiation equally in all directions at some rate
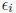
• Each surface reflects a fraction
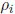of the incident radiation
• The emitted radiation from one surface falls on the other
surfaces
◦
How it gets distributed depends on geometry
◦
The fraction of light leaving patch i that ends up at patch j is the
form factor fij .
A radiation balance at each surface results in a linear equation:
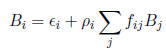
where Bi is the total radiation leaving the surface, known as its
radiosity (hence the name of the method).