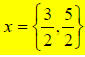Final Exam Review Form 1

Solutions

1. Solution: [B]

To solve this equation, find the LCD of the equation (in this case, LCD = 12) and
multiply both sides of the equation by the LCD to clear fractions. Then finish
solving the equation.

2. Solution: [D]

In any absolute value equation, the first task is to isolate the absolute value bars.

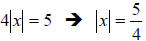
Then, split the absolute value equation into two regular equations, each with
opposites on the right side of the equal sign.

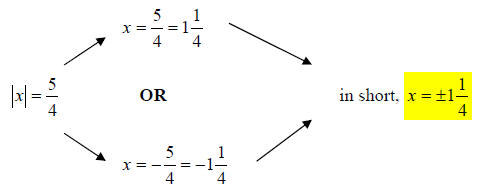
3. Solution: [B]

When solving an inequality, treat it like an equation – excepting the fact that if
you multiply or divide both sides of the inequality by a negative number, you
reverse the inequality symbol.

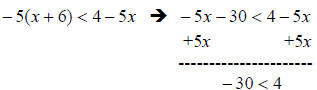
When the variables disappear from an inequality, you have a true / false
statement. If the resulting statement is true, the solution is all real numbers;
however, if the resulting statement is false, there is no solution.

Here, -30 is less than 4, so the solution is: [B] all real numbers.

4. Solution: [B]

This problem mirrors no. 4 above in technique: solve for x just like an equation –
watching out for the negative number multiplications and divisions.

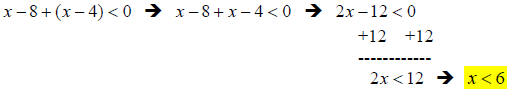
5. Solution: [C]

Here, we want to get rid of the fraction first…but we don’t have to multiply by
the fraction’s inverse all at once…we start with:


B = 5/8 (A − 8)

If we first multiply both sides by the denominator 8, then distribute the 5 to the
parentheses:

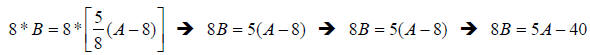
Now, finish solving for A:

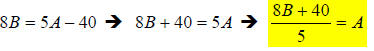
6. Solution: [A]

I am assuming that you (the student) possess a TI-83 graphing calculator…that
fact makes this problem a push-button extravaganza. The key is to know what
numbers are grouped together in the problem. The main group to be wary of is
the expression “4*10” in the exponent…these are grouped.

Notice the following calculator screen:

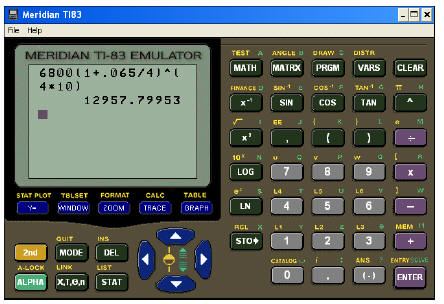
You do not need the parentheses around “.065/4”, because the natural order of
operations within that set of parentheses will take care of those numbers…but you
do need those parentheses around “4*10” because multiplication happens after
powers in the order of operations – and you need the multiplication done first
before the power is done.

Rounding to the hundredths, your answer is [B] 12,957.80.

7. Solution: [A]

The formula for the distance between two Cartesian points is:

dist. =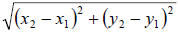

If we label the given points: (4,0) (x₁, y₁)  and (1, −5)  = (x_2, y₂) , then:

dist. =

8. Solution: [B]

The formula for the midpoint of two Cartesian points is:

midpt =

**Remember – Midpoint is an ordered pair not a single number.

If we label our points like this: (13, -11) = (x₁, y₁) and (18,6)  = (x₂ ,y₂) , then:

midpt =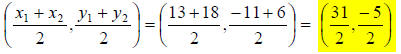

9. Solution: [B]

The formula for the slope of a line given two Cartesian points is:

slope =

Labeling our two points as ( -6, -3)  = (x₁, y₁) and ( 7,7) =  (x_2, y₂) we get:

slope =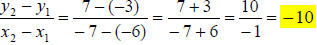

10. Solution: [C]

One way to find the slope of an equation is to solve it for “y”, or put the equation
in slope-intercept form, y = mx + b. In this form, the slope is the coefficient of x.

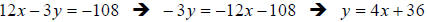
The coefficient of x is 4, therefore the slope of the line is 4.

11. Solution: [D]

The intercepts of a line are the points where the line intersects the x- and y- axes.

The x-intercept is the point where the line intersects the x axis. It is found by
setting the y = 0 in the equation of the line, then solving the equation for x:

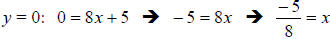
The x-intercept is -5/8

The y-intercept is the point where the line intersects the y axis. It is found by
setting the x = 0 in the equation of the line, then solving the equation for y:

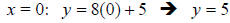
The y-intercept is 5

12. Solution: [A]

The range of a relation is the set of all y values present in the relation. (A
relation is a set of ordered pairs.)

Here, the y-values from the ordered pairs are {-3, 4, -4}, this is the range.

13. Solution: [D]

The first step is to graph the equation y = 1 + x in order to see what it is doing.
Now, notice that it is an upward sloping line that has an x-intercept of -1 and a
y-intercept of 1.

OK, domain is the set of all of the x values that you can substitute (or “input”)
into an equation and get a y back. Or, visually, it is how far left and how far right
the graph runs, excluding any gaps in the graph. Here, our graph runs as far left
as we want to go on it, and also as far right as we want to go on it (it doesn’t stop
and turn around, nor does it just stop), so the domain is all real numbers – or, in
interval notation, (-∞, ∞).

Now, range is the set of all of the y values that are possible to be “output” from a
function. Graphically, it is how far up and how far down the graph runs,
excluding any gaps in the graph. Here, the graphs is always moving up and down
(there are no ‘turn-arounds’ or stops), so the range is all real numbers or (-∞, ∞).

14. Solution: [A]

In this graph, which by the way is y = x² – 2 in case you are interested, notice that
the graph is always running to the left and to the right with no gaps or stops –
therefore the domain is (-∞, ∞).

The range, on the other hand is different. Look at how the graph goes down to y =
-2, then rises on both sides of it – or, in other words, the graph never drops under
y = -2. Also, the graph rises endlessly. This means that the range of this graph is
[-2, ∞), the bracket on the -2 indicates that the graph actually touches y = -2.

Oh, by the way…never ever bracket infinity! Why? Well, the bracket indicates
that you have reached that number…can you reach either -∞ or ∞? This would
mean that you could say what number infinity is…this is where the problem is,
infinity is an idea – neither a real nor an imaginary number.

15. Solution: [C]

A function is a relation in which each element of the domain (x value) is paired up
with exactly one element of the range (y value).

The answer is [C], and this can be easily seen using a ‘bubble mapping’, or just
mapping. Put all x values in one bubble, the domain, and all y values in the other
bubble, the range, like this…don’t repeat numbers in the bubbles – put each
number once per bubble:

The arrows match up each x with its y from each ordered pair. A function exists
when each x has only one arrow leaving it. The mapping technique is not
worthwhile if you have a graph or equation…only sets of ordered pairs work here.

16. Solution: [A]

When you are given graphs, you can use the vertical line test to determine
whether or not you have a function. If you pass vertical lines through the graph of
a function, you will not hit the function in more than one place. In graphs i), ii),
and iv); no vertical line will hit the graphs in more than one place, so they are
functions. In graph iii), however, you can pass a vertical line down through the
interior of the circle and hit the circle twice – so iii) is not a function.

17. Solution: [B]

A one-to-one function is a very exclusive type of function (it is the only type to
have an inverse function!) where not only is each element of the domain is paired
up with exactly one element of the range, but also each element of the range is
paired with exactly one element of the domain…one (domain)-to-one (range)…

The answer is [B]…to show this let’s start with a bubble mapping like we used in
15.) above, with arrows drawn:

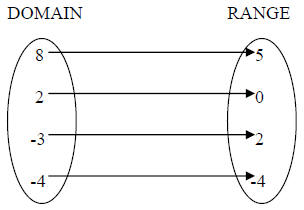
Notice that each x has exactly one arrow leaving it (which makes this relation a
function), but also notice that each y has exactly one arrow leading to it…this is
how a one-to-one function maps out. If there is more than one arrow leading to a
single y, you will not have a one-to-one function.

18.) Solution: [D]

To test a graph to see if it is a one-to-one function is to first use the vertical line
test to see that you have a function, then use the horizontal line test, if you can
pass horizontal lines through a function’s graph and hit it in at most one place,
you have a one-to-one function.

Graph i) is a function by the vertical line test, but fails the horizontal line test – so
i) is not a one-to-one function. Graph ii) is not a one-to-one function for the same
reason as i), graph iii) is not even a function. Only graph iv.) passes both line
tests and is a one-to-one function.

19.) Solution: [B]

To find f (-3), simply substitute -3 in for the x variable every time it appears
in f (x), then simplify the resulting expression.

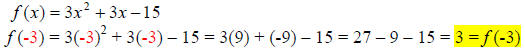
20.) Solution: [A]

The expression (f + g)(x) means to add the functions f and g together, combining
like terms.

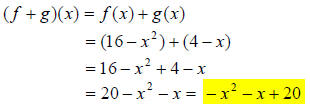
21.) Solution: [B]

The expression f ( g (x) ) is a composite function. A composite function takes one
function and inputs it directly into the x variables of another function.

In this problem, f ( g (x) ), we take the function g(x), the ‘inner’ function, and
input it into each x in the function f, the ‘outer’ function.

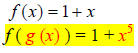
22.) Solution: [A]

The process to find the inverse of a function is four steps:

(I) Rewrite f (x) in y = notation
In our problem, this is already done – we have y = form already.

(II) Interchange x and y.
Our problem, y = 4x − 2 becomes x = 4y – 2

(III) Solve for the new y.
Just solve the equation you created in step (II) above like any other
equation.

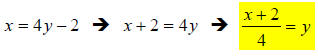
**This is the answer that is needed. Technically, there is a step four
though. Just for completeness…

(IV) Rename ‘y =’ as ‘f ^-1(x) =’
The notation f^-1(x) is called “f inverse” notation,
not “f to the negative one”.

23.) Solution: [B]

Look at the equation you are given…f (x) = -3x + 6. Remember, ‘y =’ and
‘f (x) =’ mean the same thing, so you really have the equation y = -3x + 6.
This equation is in slope-intercept form, y = mx + b, meaning that you can read
the slope (m) and y-intercept (b) right off of it and use that information to find the
correct graph.

Here m = -3 (the slope) and b = 6 (the y-intercept). So first let’s look for the
graph that crosses the y-intercept at positive 6…this eliminates choices [A] and
[D] immediately. Now, we have a negative slope - which means that as we move
to the right, the graph goes down. Only choice [B] fits that description, so [B] is
the graph we need.

**Notice that we did not need the entire -3 we found as the slope…just
the way the line is sloped (given by the sign of the slope) is sufficient in this
multiple-choice question..**

24.) Solution: [D]

In this problem, you have a number to a fractional exponent. A fractional, or
rational, exponent signifies that a power and a root are taken of the same quantity.

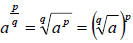, notice that either the power or root can be done first.
or in general, a rational exponent is of the form “power / root”: root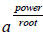
 In our problem, we have 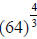which translates into either .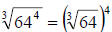

The difference is that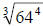 says to do the power and then the root (not the easiest
thing…what is 64⁴?)…but if we go with the 2^nd form, 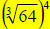, we find 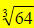first,
which is four, then we raise that number to the fourth power which is 256.

Remember, though, either of the above forms is OK to use here…they should
both give you 256.

25.) Solution: [C]

A suggested way to attack this problem is this:

First, use the negative exponent property to “move” the quantities with negative
exponents around to give them positive exponents –

• A quantity with a negative exponent in the denominator must be moved to the
numerator in order to change to a positive exponent.

• A quantity with a negative exponent in the numerator must be moved to
the denominator in order to change to a positive exponent.
Here, 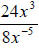will become 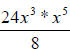, because the x in the denominator had a
negative exponent and was moved to the numerator to give it a positive exponent,
then was multiplied by the numerator. To finish, just multiply the x variables in
the numerator and finish dividing the 24 and the 8:

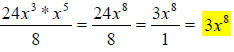
26.) Solution: [C]

To start here, let’s make use of the power of a quotient rule of exponents, if you
have a quotient (a fraction) to a power, raise the numerator and the denominator
to the power separately:

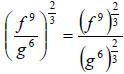
Now, you have two separate cases of a power to a power, which means that you
multiply the exponents together like this:

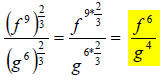
27.) Solution: [A]

In this monster, the first thing to tackle is to simplify the numerator and
denominator separately. Then we can worry about the division bar.

The numerator here is: (xy¹⁰ )(x⁴ y). To simplify it, all we have to do is to
multiply the x and y variables together (adding exponents as we go).

(xy¹⁰ )(x⁴ y)= x * y¹⁰ * x⁴ * y = x * x⁴ * y¹⁰ * y = x¹⁺⁴ y¹⁰⁺¹ = x⁵ y¹¹

The denominator here is: (x² y² )⁴ . To simplify it, just use the product to a power
rule – raise each factor in parentheses to the power outside of parentheses, then
simplify.

(x² y² )⁴ = (x² )⁴ ( y² )⁴ = x²*⁴ y²*⁴ = x⁸ y⁸

The original problem is now: 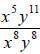. Using the division rule of exponents, we
have:

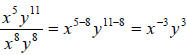which simplifies to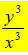

28.) Solution: [A]

Here we a chain of rational expressions, two multiplied followed by a third
divided. Let your first step be to change the division at the end to a multiplication
by inverting the rational expression that follows the division and changing the
division to multiplication, like this:

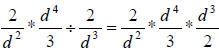
Now, make one large fraction by multiplying all of the numerators together in one
large numerator, then by multiplying all of the denominators together in one large
denominator. Then use the laws of exponents and math operations to simplify:

29.) Solution: [C]

It would be very beneficial to factor this expression before attempting to multiply
it. The reason that it is much easier to deal with factors (things being multiplied)
than it is to deal with terms (things being added and subtracted) in multiplying
and dividing rational expressions. I will show the factored forms of each
numerator and denominator first and then summarize the procedure that can be
used for each factorization.

1^st, the factored forms in the expression:

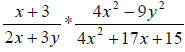factors to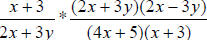

Now:

The 1^st numerator, x + 3, is already factored.

The 1^st denominator, 2x + 3y, is already factored.

The 2^nd numerator, 4x² − 9y² , factored by a difference of two squares.

The 2^nd denominator, 4x² +17x +15 , factored by trial and error.

OK, now that we have factored expressions, we can start cross-canceling.
** Remember, any numerator’s factor can cancel with any denominator’s factor –
as long as the factors match. **

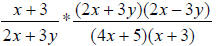cancels to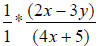which is

(We canceled the 2x + 3y and x + 3 factors above.)

30.) Solution: [A]

In adding and subtracting rational expressions, we must first get an LCD – just
like when adding number fractions (2/5 + 3/5, for example).

Here we have an LCD already, x² − 64 , and therefore can go ahead and combine
our numerators over the common denominator. Then we simplify the numerator
as much as possible.

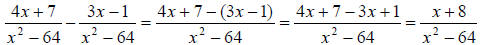
OK, once you finish the subtraction (or addition in other cases), always try to
factor the numerator and denominator in your result…while adding or
subtracting, it is possible to create factorable expressions that were not in the
original problem. If you can factor the answer you just got, see if any like factors
will cancel from numerator to denominator.

Here, the denominator can be factored by a difference of two squares, and we can
cancel a pair of like factors:

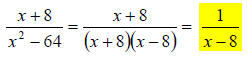
31.) Solution: [C]

Here we are asked to add two rational fractions with unlike denominators. We
must first find the LCD. To find the LCD of two rational expressions, we first
factor the denominators that we have:

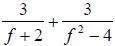with factored denominators is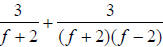

Now, make a count of the types of factors and the number of times that each
factor occurs in each denominator:

	f − 2	f + 2	DENOMINATOR FACTORS
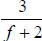	0 times	1 time
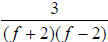	1 time	1 time
RATIONAL EXPRESSIONS

Now, find the largest number of times that each factor appears in any one
denominator. The LCD will consist of these factors:

f − 2 occurs at most once in any one denominator.
f + 2 occurs at most once in any one denominator.

So the LCD of the rational expressions is ( f + 2)( f − 2).

Now, we rewrite each fraction with the LCD. This involves putting any extra
factors needed to make the LCD in the numerator and denominator of each
fraction.

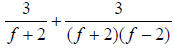becomes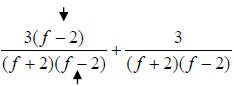

Notice the factor ( f − 2) we put into the first expression to make the LCD
happen in the denominator. Now we just simplify as in 29.)…remember to watch
out for new factors at the end of the problem. Notice how the answer took into
account that you factored the numerator at the end for completeness

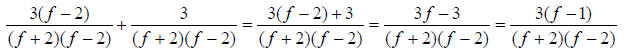
32.) Solution: [C]

To solve a rational equation, first find the LCD of all of the rational expressions
involved. Following the procedure above for finding the LCD, you should get
(x +1)(x −1) as the LCD here for these 3 rational expressions.

Once you find the LCD, we multiply each term in the equation by the LCD. This
is the “clear fractions” step of the equation solving procedure. It is best to leave
your denominators factored when you multiply by the LCD, because canceling is
much easier.

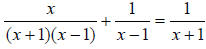when multiplied by the LCD becomes:

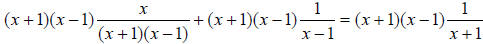
Now, cancel matching factors from numerator to denominator to get:
x + (x +1) = (x −1) , and finishing the solve for x gives us:

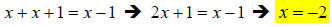
33.) Solution: [C]

The expression for direct variation is: y = k * x, where:

k is a constant of proportionality, the factor by which y changes with
respect to x.

x and y are the two variables that are changing.

In this variation problem, you are given a set of data that relates S and F in the
problem statement. Namely when S = 0.6, F = 60. We need to use this
information to find k; since k does not change in this problem, we can use the k
we find to finish the problem. To find k, just plug in S and F into a direct
variation expression and solve the resulting equation for k.

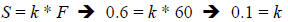
Now, we use the k we found in a new expression relating the S we don’t know to
the weight of 80 pounds (F = 80).

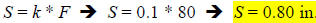
34.) Solution: [D]

In order to write a radical in exponential form, we have to use the definition
presented earlier in Problem 24.):

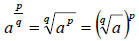,or in other terms,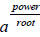

Here, we have 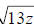, which is the quantity 13z to the 1^st power, all under a square
(2^nd) root. In order to write this as an exponent quantity, we use the “power over
root” way of thinking of rational exponents:

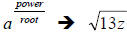becomes 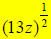** Parentheses are needed around 13z. **

35.) Solution: [A]

An rational number is a number that, when converted to decimal form, is either a
repeating or terminating decimal; also if the number can be written as a fraction of
integers (0 is not allowed in the denominator), the number is rational. If the
number fails in the above rule, it is irrational.

Answer [A] is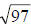 . If we perform the square root, we get 9.8488578018…

Notice that the decimal neither stops (terminates) nor does it have a
distinguishable pattern (repeats), so [A] is irrational.

36.) Solution: [D]

To simplify this radical expression, first factor the radicand (quantity under the
radical symbol) into prime numbers. 75 factors down into 3 * 5 * 5, so the radical
becomes.

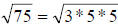
Now, the way to reduce a radical is this: Once you have factored the radicand,
count the number of times each factor occurs. Then pull like factors out in groups
equal to the index on the radical (for square roots, pull factors out in groups of
two; for cube roots, pull in groups of three; etc.). For each group you pull out, put
one of the group outside the radical and then multiply that number by the radical.

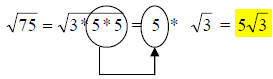
One group of two 5s come out from the radical; the 3 must stay.

37.) Solution: [C]

Here, we start by factoring the radicand to prime numbers again.

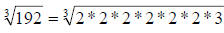
Notice that this time, we have a cube root, so we pull the matching factors in
groups of three this time. Again, if there are not enough of a factor to make a
complete group, leave them under the radical.

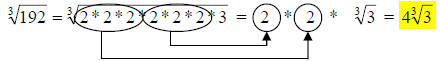
38.) Solution: [A]

Here we are asked to simplify another radical…in this case however, we can
notice that we are asked to take the square root of a negative number. This is not
possible in the real number system, so we use a new quantity – the imaginary
unit i – to allow is to work these types of problems.

The imaginary unit is defined as i = .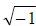

To use the imaginary unit, we first rewrite the negative radicand as

“-1” * a positive number

we can now separate the “-1” from the positive number, giving it its own radical
sign. Then, we can substitute the letter i in for 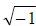. In our problem:

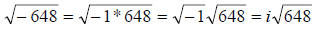
To finish, continue to factor the positive number (now under its own radical) into
primes, and pull out the appropriate groups as in the two previous problems.

39.) Solution: [D]

This problem is simplified in the same way as the previous three questions, but
now we have variables to work with. Here, just list them out in multiplication and
group them in the same way as the prime factors.

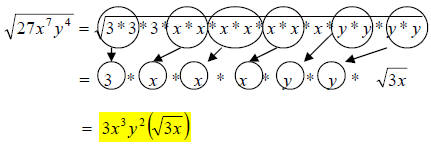
40.) Solution: [B]

This is similar to the others we have done already…factor, list out, and group.

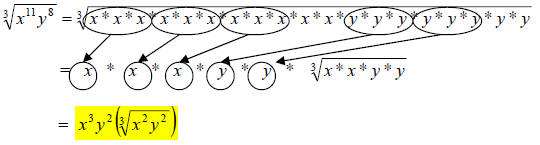
41.) Solution: [C]

Rationalizing the denominator means to remove the radical term(s) from the
denominator by multiplying the entire fraction by another radical expression that
causes the denominator to become a perfect square, perfect cube, etc.

Here, we have a denominator of 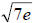. This implies that in order to get rid of the
radical, we have to multiply by another radical that will give us a perfect square
under our radical (in order to cancel out the square root that we have now).

The simplest way is to multiply our 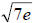by another 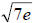to make (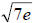)², or
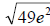, which reduces back to 7e. Remember though, we multiply the numerator
and denominator by the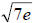 , like so:

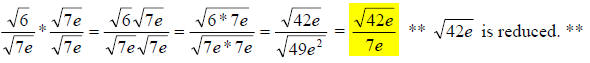
42.) Solution: [C]

Here, we follow the same technique as 41.), with one exception…we cannot use a
single radical term to cancel the denominator radical in 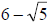. We have to use
what is called a conjugate, a binomial term that creates a difference of two
squares pattern, (a + b)(a − b) , when multiplied by another binomial. These two
binomials are called a conjugate pair.
Since our denominator is 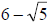, its conjugate is 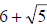. FOILing these two
binomials will remove the radical from the denominator expression:

Now, let’s use the conjugate in the full problem:

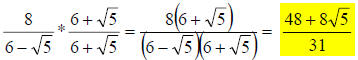
** Don’t forget to distribute the 8 through the numerator’s parentheses. **

43.) Solution: [D]

In completing the square, once you get the 1x² and x terms on the same side – then
take half of the coefficient of x, square it, and add that number to both sides of the
equation.

Here, the coefficient of the x term is 4…half of the 4 is 2, then 2 squared is 4, the
number we have to add to both sides of the equation.

44.) Solution: [C]

The device we use for this question is called the discriminant, the radicand in the
Quadratic Formula. The power of the discriminant is to tell us the types of the
solutions that we can expect, not what the solutions actually are…that is done by
the whole Quadratic Formula.

The discriminant is b² − 4ac :

• If the discriminant is positive, two unequal real roots exist.
• If the discriminant is zero, two equal real roots exist.
• If the discriminant is negative, two unequal imaginary roots exist.

Using our information, a = 5, b = 6, and c = 1:

b² − 4ac = 6² − 4(5)(1) = 36 − 20 = 16

Since the discriminant is positive, two unequal real roots exist.

45.) Solution: [B]

To solve a quadratic equation, first isolate a zero on one side of the equation.
This is called standard form of a quadratic equation, ax² + bx + c = 0 , with a ≠ 0 .

Here, let’s subtract 12 from each side to start:

Then factor the left side (by trial and error in this case):

Now, we use the zero-product property, if we have several factors that multiply
out to be zero – at least one of them must be a zero. We apply the property by
setting each factor equal to zero on its own and solving each new equation for x.

(3x − 4)(x + 3) = 0

3x − 4 = 0 OR x + 3 = 0

x = 4/3 OR x = −3 , so the two solutions are x = {-3,4/3 }

46.) Solution: [A]

The quadratic equation is already in standard form, but as you have probably seen
– it does not factor with integers. Also, completing the square may not be the best
choice (but it will work) since when you divide by 2 to clear the x², you create a
fraction out of the constant 1.

In my example, I will use the Quadratic Formula: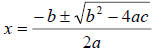

In this case, a = 2, b = 8, and c = -1:

Reducing the radical 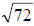, we get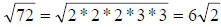

So your answer at this point is: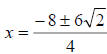  , however, we can factor the
numerator by pulling a 2 out of the -8 and the 6 that is multiplied by the square
root of 2, but you cannot factor the 2 out from under the radical. Doing the
factoring and canceling we get:

47.) Solution: [C]

This is a quadratic equation that is prepared for the square root property method
of solving. In this method, you first isolate a perfect square on one side of the
equation – here (2x − 4)² - and then take the square root of both sides, like this:

Notice the plus/minus sign – whenever you take an even root (square root, fourth
root, etc.) of a variable, the other side of the equation gets the plus/minus for free.
Also see that the left side became just what was being squared after we took the
squared root…this always happens.

Now we finish solving for x, be careful that when you add the four to both sides,
you do not directly add it to the plus/minus 1, just put it to one side of it (I
recommend the left), watch:

Then divide everything by 2 to finish: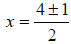or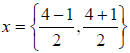

or