Algebra 1 Unit Descriptions & Learning Targets
Unit 3: Systems of Linear Equations
In the previous unit, it was determined that the graph of a linear equation is a
line. Parallel and perpendicular lines will be revisited to demonstrate systems
of equations. Next, it is a natural to then investigate where two lines might
intersect in the coordinate plane. A simultaneous system of linear equations is
then defined in order to answer this question. The solution set of a system of
linear equations is defined as the set of ordered pairs that satisfy both
equations. This concept is connected to the intersection of two lines in the
coordinate plane. Examples of the intersection of two linear functions are
discussed, including cases where the graphs of the linear functions are parallel
lines (no solution), or the same line (infinitely-many solutions).
The equations used in a linear system often are written in
standard form, which is defined as Ax + By = C. The substitution and linear
combinations
methods are then explored as a way of solving systems of linear equations. Empty
and infinite solution sets are discussed in the context of substitution and
linear combinations. These methods are also used to solve systems of linear
equations in a real world context, and the solutions of these systems are
interpreted in that context.
As stated in the previous unit, a root of a function is a value of x that makes
the function have a value of 0, or in other words, the value that makes y = 0.
A more geometric interpretation is that a root is the x-value of the
intersection of the given function and the horizontal line y = 0. This concept
is an example
of the solving part of system of linear equations. In other words, the solution
to any equation in one variable can be viewed as the x-value of the intersection
of two functions (e.g. the solution to 2x -1= 5 - x is the x-value of the
intersection of y = 2x -1 and y = 5 - x). A wide variety of examples of this
concept are explored.
| # | Learning Targets | Stand ard |
Textbook | Active Practice |
| 3A | Explain the meaning of a system of
linear equations and a solution to a system of linear equations |
9.0 | 8.1 pg 358 | |
| 3B | Use knowledge of slopes to identify
systems of parallel and perpendicular lines as well as write equations for lines that are parallel or perpendicular and explain |
9.0 | 7.8 pg 338-341 # 1- 41 |
|
| 3C | Explain the reason why not all systems of equations have the same number of solutions. | 9.0 | 8.1 pg 359 # 21 - 23 |
|
| 3D | Graph a system of linear equations and estimate the solution based on the graph. | 9.0 | 8.1 pg 358 #15 – 20 |
|
| 3E | Verify that an ordered pair is a
solution to a system by substituting the x and y coordinate into each equation of the system. |
9.0 | 8.1 pg 358 #1 - 8 |
|
| 3F | Solve a system of equations by
substituting one equation into the other and solving for x and y coordinate of the solution and explain the process |
9.0 | 8.2 pg 365 #1 – 21 |
|
| 3G | Solve a system of linear equations
using linear combinations and explain the process of doing so. |
9.0 | 8.3 pg 371 #1 - 30 |
|
| 3H | Solve real world problems by setting
up algebraic systems of equations and solving for the two unknowns. |
15.0 | 8.2 pg 365 22 – 27 8.3 pg 371 31 – 36 8.4 – 8.6 all |
|
| 3I | I can justify my reasoning for
choosing one method of solving a system of equations over another method, while still explaining how all methods could lead to the same solution. |
9.0, 15.0 | n/a | Mini White Boards |
Essential Standards:
9.0: Students solve a system of two linear equations in two variables
algebraically and are able to interpret the answer graphically. Students are
able to solve
a system of two linear inequalities in two variables and to sketch the solution
sets.
15.0: Students apply algebraic techniques to solve rate problems, work problems,
and percent mixture problems.
Supporting Standards:
6.0: Students graph a linear equation and compute the x- and y- intercepts
(e.g., graph 2x + 6y = 4). They are also able to sketch the region defined by
linear
inequality (e.g., they sketch the region defined by 2x + 6y < 4).
7.0: Students verify that a point lies on a line, given an equation on the line.
Students are able to derive linear equations by using the point-slope formula.
8.0: Students understand the concepts of parallel lines and perpendicular lines
and how those slopes are related. Students are able to find the equation of a
line perpendicular to a given line that passes through a given point.
24.0: Students use and know simple aspects of a logical argument.
25.0: Students use properties of the number system to judge the validity of
results, to justify each step of a procedure, and to prove or disprove
statements.
Unit 4: Introduction to Quadratic Equations
Another important type of function studied in this course is a quadratic
function. A quadratic function is a function defined by an equation of the form
y = ax2 + bx + c. This is called the standard form of a quadratic
function. Function tables are used to build the basic shape of the graph of
quadratic
functions and demonstrate that not all graphs are linear. Basic components of
the graph are identified, including the vertex, axis of symmetry, and roots.
The difference between the number of roots of a linear function and a quadratic
function is identified and the idea of “double root” and “no real roots” are
introduced. Simple transformations of the parent graph are
shown to illustrate the relationship of the equation and the graph. The factored
form of a
quadratic function is then introduced as y = a(x - p)(x - q) . It is observed
that p and q are the roots of the function, and that the x-coordinate of the
vertex
of a quadratic function lies halfway between the roots of the function. Given a
quadratic function in factored form, the roots and vertex are found, and the
graph of the function is drawn. Once factored form of the quadratic is
introduced, polynomial multiplication is demonstrated as a means to move from
factored form to standard form of the quadratic.
| # | Learning Targets | Stand ard |
Textbook | Active Practice |
| 4A | Differentiate between the graph of a
linear function and the graph of a quadratic and explain the definition of a quadratic function |
21.0 | ||
| 4B | Graph the parent function y = x2 and identify the major components of the graph. | 21.0 | ||
| 4C | Identify the vertex and the axis of
symmetry of the graph of a quadratic function and explain how these influence the shape of the quadratic |
21.0 | ||
| 4D | Use function tables to graph
quadratic functions and explain the connection to graphing linear functions by the same method. |
21.0 | ||
| 4E | Identify the roots/solutions/zeros of
the quadratic function when given a graph of the function. |
21.0 | ||
| 4F | Determine the number of real solutions when given the graph of a quadratic equation | 21.0 | ||
| 4G | Explain the relationship between the
factored form of a quadratic function and the roots of that same function. |
21.0 | ||
| 4H | Find roots/zeros/solutions of a
quadratic function in factored form and use that information to sketch a graph of the function. |
21.0 | ||
| 4I | Multiply two polynomials to determine
the relationship between factored form and standard form of the quadratic. |
10.0 | ||
| 4J | Explain why quadratic equations ware
used to represent the height of a launched or falling object. |
21.0, 23.0 |
Essential Standards (CA):
21.0: Students graph quadratic functions and know that their roots are the
x-intercepts.
10.0: Students add, subtract, multiply, and divide monomials and polynomials.
Students solve multi-step problems, including word problems, by using these
techniques.
Supporting Standards:
16.0: Students understand the concepts of a relation and a function, determine
whether a given relation defines a function, and give pertinent information
about given relations and functions.
23.0: Students apply quadratic equations to physical problems, such as the
motion of an object under the force of gravity.
24.0: Students use and know simple aspects of a logical argument
25.0: Students use properties of the number system to judge the validity of
results, to justify each step of a procedure, and to prove or disprove
statements.
Unit 5: Solving Quadratic Equations
The concept of a solution to an equation in one variable is once again linked
with the intersections of the graphs (e.g. the intersection of
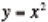and
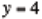is
the solution to the equation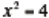
). In particular, it is discussed that the
solutions to
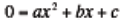represent the roots of the function
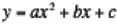. The quadratic formula is then introduced as a way of determining the solutions
to a quadratic equation, or the roots of a quadratic
function. It is emphasized that the equation must be written in standard form to
use the quadratic formula. The quadratic formula is used to solve a wide
variety of quadratic equations, including problems modeling the motion of a
launched or falling object. The zero product property is introduced and used as
a
means to find the solutions to quadratic equations that are in factored form.
Using the found roots of a quadratic function, sketches of the graph of the
function are created, and the relationship among solutions, roots, and
x-intercepts is communicated.
| # | Learning Targets | Stand ard |
Textbook | Active Practice |
| 5A | Explain the relationship between the
solution of a quadratic equation and the graph of the related function. |
21.0 | ||
| 5B | State the quadratic formula and explain how to use it to solve quadratic equations | 19.0 | ||
| 5C | Solve quadratic equations using the quadratic formula. | 20.0 | ||
| 5D | Find the discriminant of a quadratic
equation and use it to explain the difference between real and non- real solutions of quadratics. |
19.0, 20.0 | ||
| 5E | Explain the conditions for when a
quadratic equation has no real solutions, one real solution, or two real solutions. |
20.0 | ||
| 5F | Solve problems related to the motion
of a launched or falling object using the quadratic formula and explain the connection between solutions and landing on the ground. |
23.0 | ||
| 5G | Simplify radicals to help find the approximate and exact solutions to a quadratic equation. | 19.0 | ||
| 5H | Explain the Zero Product Property and use it to solve quadratic equations in factored form. | 14.0 | ||
| 5I | Identify the vertex of a quadratic
equation when given the two roots/zeros/solutions of the equation. |
14.0, 20.0 | ||
| 5J | Explain the relationship among solutions, roots, and x-intercepts of a quadratic function. | 14.0, 20.0 | ||
| 5K | Given the two roots (or
x-intercepts), I can sketch the graph of the function, write an equation for the function, and verify by solving the equation for the roots. |
21.0 |
Essential Standards (CA):
14.0: Students solve a quadratic equation by factoring or completing the square.
19.0: Students know the quadratic formula and are familiar with its proof by
completing the square
20.0: Students use the quadratic formula to find the roots of a second-degree
polynomial and to solve quadratic equations.
23.0: Students apply quadratic equations to physical problems, such as the
motion of an object under the force of gravity.
Supporting Standards:
21.0: Students graph quadratic functions and know that their roots are the
x-intercepts.
22.0: Students use the quadratic formula or factoring techniques or both to
determine whether the graph of a quadratic function will intersect the x-axis in
zero, one, or two points.
24.0: Students use and know simple aspects of a logical argument.
25.0: Students use properties of the number system to judge the validity of
results, to justify each step of a procedure, and to prove or disprove
statements.