Exploring Similar Triangles
Objectives: To make conjectures about the sides,
perimeters, and areas of one triangle
and the triangle that is constructed from the midpoints of the sides of the
original triangle.
Materials: Geometer’s Sketchpad, overhead projector for computer (this
could be easily
adapted for the TI-92), class set of computers with Geometer’s Sketchpad on
them.
Role of Technology: We will use the Geometer’s Sketchpad to construct
triangles and
their midpoints. Sketchpad will also calculate the length of the sides of the
triangles, the
perimeter and the area for us. Constructing various triangles on Geometer’s
Sketchpad
will allow us to make conjectures that we can apply to all triangles.
Previous knowledge base: Students have prior knowledge of triangles,
length,
midpoint, perimeter, and area. Students also have some experience with the
Geometer’s
Sketchpad.
Lesson:
• Set Establishment (5 - 7 minutes)
Tell the student that we are going to work with Geometer’s Sketchpad today to
make
important discoveries regarding triangles. Ask them if they recall how to find
the
midpoint of a line. The midpoint is the actual “middle point” of a line such
that the
length from the midpoint to each endpoint is the same. The formula to find the
midpoint
of the line with endpoints P1(a,b) and P2(c,d) is
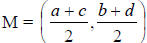. Next ask the
students how to find the perimeter and the area of a triangle. To find the
perimeter, add
the length of the three sides. Area of a triangle is
(base)(height). We will not be
computing these formulas by hand today, we will let Geometer’s Sketchpad compute
them for us.
• Creating the First Triangle (3 minutes)
Open up Geometer’s Sketchpad. While performing the following procedures, tell
your students what you are doing explicitly so that they can follow along.
Choose the
point (it looks like a dot on the left side of the screen). Make three points on
the
screen. Now choose the arrow and select all three points by holding down SHIFT
and
clicking on each point. Now choose SEGMENT from the CONSTRUCT menu. We
have just constructed a triangle. Ask if there are any questions.
• Constructing a Second Triangle from the Midpoints of the First (7 minutes)
Now, using the arrow again, select the three sides of the triangle we have
constructed.
From the CONSTRUCT menu again, choose POINT AT MIDPOINT. A point
appears at the midpoint of each segment. Now with the SHIFT key held down,
select
our three midpoints. Then, choose SEGMENT from the CONSTRUCT menu. We
have just constructed a smaller triangle inside our original triangle using the
midpoints of the first triangle as the vertices of the second. Ask if there are
any
questions and quickly walk around the room to make sure everyone has the right
picture.
• Analyzing the Measures of the Angles and Sides (15 minutes)
Using the “hand” on the left toolbar, label your points.
This will make it easier to
analyze our measurements. Now use the arrow again and select the sides of the
first
triangle. Then, choose LENGTH from the MEASURE menu. This calculates the
length of the sides of the triangle. Repeat this for the second triangle. Ask
the
students if they notice any relationship between the length of the sides of the
larger
triangle and the length of the sides of the smaller triangle. If they cannot
come up
with any conjectures, tell them to specifically look for a relationship between
the
length of the side of the larger triangle and the length of the side of the
smaller
triangle that is parallel to it. For example, in the picture below the students
should
look for a relationship between side AC and side EF. The students should notice
that
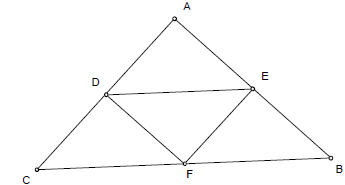
the length of the each side of the larger triangle is
twice the length of the side of the
smaller triangle that is opposite it (and also parallel to it). So in this
example, AC is
twice as long as EF, AB is twice DF, and CB is twice DE. Now let’s look at the
measures of the angles in each triangle. To measure the angle, select the three
points
that define the angle in order. For example, if I wanted to measure angle A in
the
picture above, I would select point C, then A, then B (all while holding the
SHIFT
button as before). Then choose ANGLE from the MEASURE menu. Another way to
get this same angle would be to choose points D, A, and E since ∠ CAB is equal
to
∠ DAE. Repeat this procedure for the angles at the vertices of each triangle.
There
should be a total of 6 angle measures. For review, ask the students what the sum
of
the three angles in each triangle should be (180°). Once the students have
calculated
the measures of all the angles, ask if they notice anything of interest about
the angles.
The students should notice that the opposite angles are equal. In our example
above,
∠ A = ∠ F, ∠ B = ∠ D, and ∠ C = ∠ E.
• Analyzing the Perimeters and Areas of the Triangles (15 minutes)
Now we will look at the perimeter and area of each of our triangles. Select the
three
vertices of the larger triangle. Then choose POLYGON INTERIOR from the
CONSTRUCT menu. This should color the interior of the triangle. Now choose
PERIMETER and AREA (one at a time) from the MEASURE menu. Repeat for the
smaller triangle. We will now compare the areas and perimeters of the two
triangles.
It may be difficult to understand what is happening here since the students will
only
have two measurements to compare for the perimeter and two to compare for the
area. Make a table on the board and ask students to give you their information
to fill
the chart. With a lot of data from the class, the students should be able to see
the
relationship between the triangles. A sample table is below (you may need more
than
4 entries).
| Perimeter (Big Triangle) |
Perimeter (Small Triangle) |
Area (Big Triangle) |
Area (Small Triangle) |
 |
 |
||
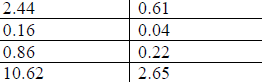From the table, the students should conclude that the
perimeter of the larger triangle
is twice the perimeter of the smaller triangle and that the area of the big
triangle is 4
times the area of the small triangle. It would be good for the students to drag
the
triangles around a bit to see that this really works.
• Assignment (5 minutes)
Hand out the following worksheet for homework and ask the class if there are any
further questions.
In the triangle below, each interior triangle is
constructed from the midpoints of the
triangle it is inside. You are given the following measurements.
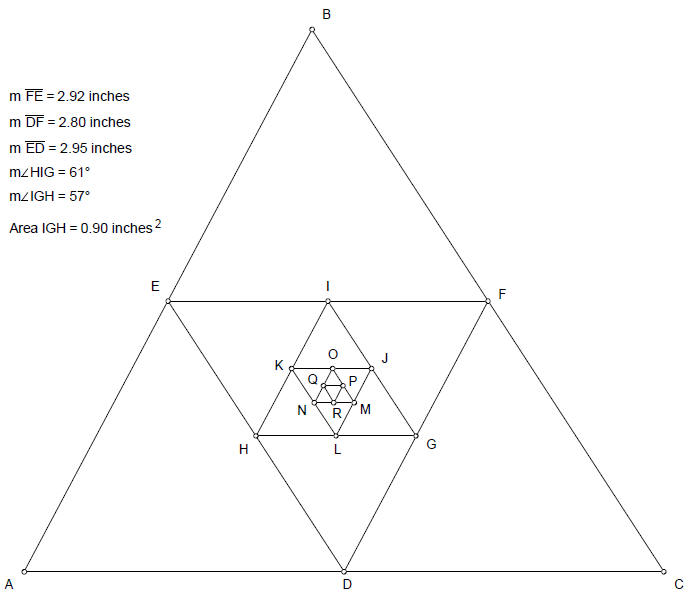
Calculate the following lengths.
1. AD
2. LJ
3. QP
4. HK
Calculate the following angles.
5. ∠ CAB
6. ∠ QPR
7. ∠ NOM
8. ∠ KLJ
9. ∠ IHG
Calculate the following perimeters.
10. ABC
11. GHI
12. QPR
Calculate the following areas.
13. ABC
14. QPR
15. JKL