Operations on Fractions

Fractions can be thought of as splitting a whole
into a number of parts and taking a certain
number of parts.

How many cents is a dollar split into?
(100)
What fractional part of a dollar is 70 cents?
(70/100 or 7/10)

As another example, the fraction 3/8 is saying

we take 3 parts out of 8.

We can draw pictures of this and other
fractions with a box representing a whole, the
smaller parts of the box representing the
number of pieces the whole is split into (8), and
the shaded region representing the number of
pieces we are interested in (3).

This is 3/8

You may remember that the tops of fractions
are called numerators and the bottoms of
fractions are called denominators. We can add
or subtract the fractions only when the
denominators are the same. We change one
fraction or both fractions so they have the same
denominators. For example, when we add

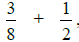we change the

We do this by multiplying:

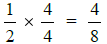
We multiply by 4/4, which is equal to 1.
Multiplying by 4/4 (or by 1) does not change
the value of the fraction, just its appearance.

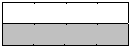
This is 1/2

This is 4/8, also 1/2

The amount shaded in the box on the right has
not been changed, only the number of pieces
that it has been split into.

Then, we can add: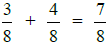

This is 7/8 (the result).

When we multiplied 1/2 by 4/4, we multiplied
the tops, put that result on top, then multiplied
the bottoms, and put that result on the bottom.

That’s all you do when multiplying fractions.
For example,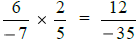

Occasionally, it is worthwhile to change a
fraction to what is called lowest terms.
This means dividing out common factors from
the numerators and the denominators. A
fraction such as 24/32 has a common factor of 8
in the numerator and the denominator.
So, we can divide the 24 by 8 and the 32 by 8
to get 3 on top and 4 on the bottom.

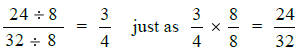
Dividing two fractions, dividing a fraction by a
whole number, or dividing a whole number by
a fraction can all be done the same way.

Division is multiplication by the reciprocal.
The reciprocal is obtained by flipping
(changing) the numerator and the denominator.

As an example, the reciprocal of 9/4 is4/9

So, to do 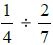we can write

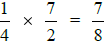
Think of a sale where everything is half off. To
get the sale price of an item that was $56.00,
for example, you can divide by 2, or you can
multiply by 1/2 Are the results the same?

Operations on Fractions

Practice Problems
Multiply:

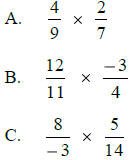
Add:

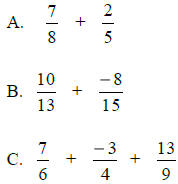
Subtract:

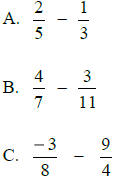
Divide:

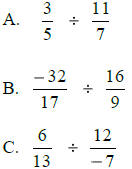
Answers

(Answers which follow the equal sign
take the first answer and write it in lowest terms.)

Multiplication:

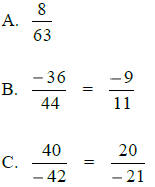
Addition:

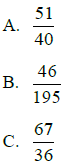
Subtraction:

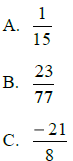
Division:

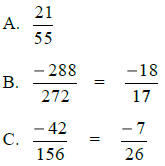
More Practice Problems

Answers (Answers which follow the equal sign
take the first answer and write it in lowest terms.)