Solutions for Math 312-A Problem Set #1

Assignment

page 23: Exercises #1, 2, 4, 7, 8, 11, 12, 14, 18, 19, 48, 49, 50, 52

Solutions

page 23, #1:

For n = 5, 8, 12, 20, and 25, find all positive integers less than n and relatively prime to n.

page 23, #2:

Determine gcd(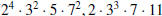) and lcm().
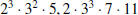The GCD takes the smallest exponent and the LCM takes the largest exponent for each prime.
The GCD is 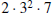and the LCM is .

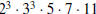page 23, #4:

Find integers s and t such that 1 = 7 · s + 11 · t. Show that s and t are not unique.

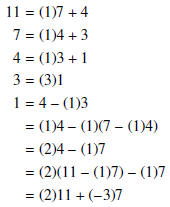
So s = −3 and t = 2 is one solution. For integer m, we also have that s = −3 + 11m and t = 2 − 7m is a solution.

page 23, #7:

Show that if a and b are positive integers, then ab = lcm(a, b) · gcd(a, b).

For any prime p that divides either a or b, the LCM contains the larger power of p and the GCD contains the
smaller power of p; their product yields the total number of factors of p in ab; therefore by unique factorization
the product of the LCM and the GCD is ab.

page 23, #8:

Suppose a and b are integers that divide the integer c. If a and b are relatively prime, show that ab divides c.
Show by example, that if a and b are not relatively prime, then ab need not divide c.

Let p be any prime and let be the largest power of p dividing a. Then since a and b are relatively prime, p
does not divide b and is the largest power dividing ab. Since a divides c, then 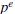divides into c. Similarly for
primes dividing into b. Therefore the prime powers in the factorization of ab divide into c and so does ab.

Let a = 4, b = 6, and c = 12. Then a and b divide c, but ab = 24 does not.

page 23, #11:

Let n be a fixed positive integer greater than 1. If a mod n = a' and b mod n = b', prove that (a + b) mod n =
(a' + b') mod n and (ab) mod n = (a'b') mod n.

Let and 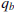be integer quotients

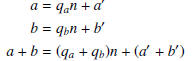
and the remainder upon division by n is the same for both sides; (a + b) mod n = (a' + b') mod n.

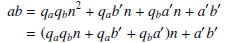
and the remainder upon division by n is the same for both sides; (ab) mod n = (a'b') mod n.

page 23, #12:

Let a and b be positive integers and let d = gcd(a, b) and m = lcm(a, b). If t divides both a and b, prove that t
divides d. If s is a multiple of both a and b, prove that s is a multiple of m.

Since d is a linear combination of a and b, if t divides into a and b it also divides into d.

If m does not divide into s, then it leaves a nonzero remainder r. Since a and b both divide m and s, then a and
b divide into r. But r < m contradicting the choice of m as least common multiple. Therefore m does divide s.

page 23, #14:

Show that 5n + 3 and 7n + 4 are relatively prime for all n
Any common divisor also divides into 1 = 7(5n + 3) − 5(7n + 4).

page 23, #18:

Let be primes. Show that 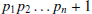is divisible by none of these primes.
For each prime the remainder is 1, not 0.

page 23, #19:

Prove that there are infinitely many primes.

Suppose not and that there are only n primes. By the previous exercise we can create a number not divisible by
any of them. It’s prime factorization must contains primes other than the ones we started with, a contradiction.

page 23, #48:

Let S be the set of real numbers. If a, b ∈ S , define a ~ b if a − b is an integer. Show that is an equivalence
relation on S . Describe the equivalence classes of S .

Reflexive: For any a, a − a = 0 is an integer.

Symmetric: If a − b = n ∈ Z, then b − a = −n∈ Z.
Transitive: If a − b = m ∈ Z, and b − c = n ∈ Z, then a − c = (a − b) + (b − c) = m + n∈ Z.

The positive numbers in an equivalence class all have the same fractional part and the negative numbers have its
complement.

page 23, #49:
Let S be the set of integers. If a, b ∈ S , define aRb if ab ≥0. Is R an equivalence relation on S ?
No. Let a = −1, b = 0, and c = 1. Then a~ b and b ~c but it is not true that a ~ c, so R is not transitive.

page 23, #50:
Let S be the set of integers. If a, b ∈ S , define aRb if a + b is even. Prove that R is an equivalence relation and
determine the equivalence classes of S .

Reflexive: a + a = 2a is even.
Symmetric: If a + b is even, then so is b + a = a + b.
Transitive: If a + b and b + c are even, then so is (a + b) + (b + c) − 2b = a + c.

There are two equivalence classes: the odd integers and the even integers.

page 23, #52:
Prove that none of the integers 11, 111, 1111, 11111, . . . is a square of an integer.
They are all equal to 3 mod 4. The squares of even integers 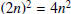are equal to 0 mod 4 and the squares of
odd integers are equal to 1 mod 4.