Inequalities
Faculty Name: Sandra H. Jones
School: Weddington Math, Science,
and Technology Academy
Grade Level: 6th
Teaching objective(s):
Interpret and write inequalities
Instructional Activities:
Teacher Will:
1. Ask students is there ever a reason that we should have to use
inequalities. (Response: when we don’t know exactly what an expression is
equal to).
2. Ask students to give real-life examples of
inequalities. (Response: amusement
park; alcohol and cigarette purchases; express check-out)
3. Display and discuss inequality signs.*Remind students
that inequalities are
read from left to right.)
4. Display simple inequalities and have volunteers read:
Ex:
x< 4 –is less than
x> 4 – is greater than
x ≤ 4 – is less than or equal to
x ≥4 – is greater than or equal to
5. Remind students of the situations that were discussed
earlier. Discuss which
word/words in the situations told them or gave them a clue for which
inequality to use.
6. List student given words on transparency. (Possible responses: at least, at
most, minimum speed, maximum speed)
7. Display inequality word problems, have student volunteers write the
inequality using numbers, variables and the inequality sign. (problem: A
number less five is greater that 7 Answer: x –5> 7)
8. Distribute and explain “Inequality Match-Up” to groups. Allowing students
about 5 minutes to complete activity. Observe and assist students as needed.
9. Summarize lesson by explaining that using riddles they can also solve
inequalities. Explain that the solution must satisfy all statements in the
riddle.
Riddle#1 “I am thinking of a natural number that is greater than 7 but less
than 10. When I multiply this number by 9, the answer is a perfect square.
(Response: 7<x<10; x =9)
Riddle #2: “I am thinking of an integer that is greater than 2 but no bigger
than 9. If I add 3 ¾ to this integer, the result is a rational number that
cannot
be smaller than 12 or more than 13. (Response: 2< x ≤ 9; 9+3 3/4=12 ¾;x =9 )
Materials and Resources
Overhead Projector
Transparency
“Inequality Match-Up” game
Assessment
1. Teacher observation: observe students and assist as they work in groups to
complete game
2. Check for accuracy of riddle.
Transparency #1:
1) A number less 5 is greater than 7.
x-5>7
2) A number greater than or equal to -2.
X ≥2
3) A number greater than -2, but less than or equal 4.
-2 < x ≤ 4
Transparency #2:
1) I am thinking of a natural number that is greater than 7 but
less than 10. When I multiply this number by 9, the answer is
a perfect square.
7< x <10 ( answer x=9) (9 x 9= 81;
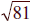 = 9)
= 9)
2.) I am thinking of an integer that is greater than 2 but no bigger
than 9. If I add 3 ¾ to this integer, the result is a rational number
that cannot be smaller than 12 or more than 13.
2< x ≤ 9; (answer: x=9); (9 + 3 ¾ =12 ¾)
“Inequality Match-Up”
Directions: Each group will be given a set of 30 index cards:
fifteen (15) with inequalities and fifteen (15) with the inequalities
written in word format. After all cards have been shuffled and
turned face down, students will take turns flipping cards matching
the inequality with the word format. Student with the most matches
wins.
| 6 + m < 2 | Six plus a number is < 2 |
| 5k ≥ 25 | five times a number is greater than
or equal to twenty-five |
| 9j ≤18 | A number times nine is less than or equal to eighteen |
| C – 2 ≤ 5 | Two less than a number is less than or equal to five |
| 2a + 3 < 7 | Three more than a number times two is less than seven |
| 7r + 5 > 19 | Five more than seven times a number is greater than nineteen |
| 4b -2 > 10 | Two less than a number times four is greater than ten |
| 8x – 3 ≥ 13 | Three less than a number times eight is greater than or equal to thirteen |
| 3y – 11 > 1 | Eleven less than three times a number is greater than 1 |
| 3f > 15 | Three times a number is greater than fifteen |
| m + 3 <6 | Three more than a number is less than six |
P – 8 ≤
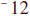 |
Eight less than a number is less than or equal to negative twelve |
| 4b ≥ 16 | A number times four is greater than or equal to sixteen |
| S + 12< 11 | Twelve more than a number is less than eleven |
T + 4 >
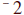 |
Four more than a number is greater than negative two |


