Math 12 Homework Solutions

1. Let f(x) = -2x² - 12x + 5. Find

(a) the x- and y-intercepts

x-intercepts:

The x-intercepts are the solutions of 0 = -2x² - 12x + 5. Since the
factorization is not immediately apparent, we will use the quadratic
formula to find the roots.

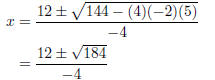
So the x-intercepts are and x.

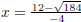y-interceps:

y = -2(0)² - 12(0) + 5 = 5

So the y-intercept is y = 5.

(b) the axis of symmetry.

(c) the vertex.

We know that the vertex is contained on axis of symmetry x = -3.
So the vertex is (-3, f(-3)) = (-3, 23).

(d) Is the vertex a max or a min?

We know that a = -2, so the parabola is downward opening and the
vertex is a maximum.

2. Find the equation y = ax² + bx + c of the quadratic function with vertex
(-2, 3) and passing through (2,-1).

We know that any quadratic function can be expressed in the form f(x) =
a(x-h)²+k where (h, k) is the vertex of the parabola. Using the fact that
we want the vertex to be at (-2, 3), we therefore get that:

y = a(x + 2)² + 3:

So all that remains is to find the value of a. To do this, we use the fact
that (2,-1) is on the graph of f.

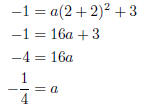
So putting this value of a into the function, we get:

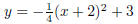
3. Setting up equations.

(a) If the area of a rectangle is 30cm, express the perimeter as a function
of width.

We want an equation for the perimeter P. So we start by writing the
function in terms of two variables:

P = 2w + 2L

We also know that the area of the rectangle is 30cm, so we have the
equation 30 = wL. We now solve this equation in terms of L to get
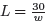and substitute this back into the function P. This gives

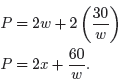
b) A rectangle is inscribed in a circle of radius 10. Express the perimeter
as a function of width.

We want an equation for the perimeter P. So we start by writing the
function in terms of two variables:

P = 2w + 2L.

We now need to find a relationship between the variables w and L,
and the only other information we have is that the radius of the circle
is 8. To understand how we will get the relationship, I slightly change
our picture.

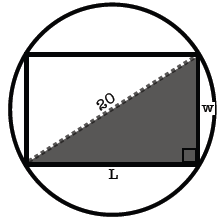
We now see more clearly that the diameter, w and L are the sides
of a right triangle. Using the Pythagorean Theorem, we see that
20² = w² + L² . We now solve this equation in terms f L to get L =
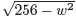(Why didn't I choose ?) and substitute
this ak into the function P. This gives

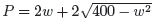
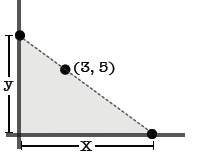
(c) A right triangle has vertices at the origin and at the points (x, 0)
and (0, y) (with x and y positive). If the hypotenuse of the triangle
passes through the point (3, 5), express the area of the triangle as a
function of x.

We want an equation for the area A. So we start by writing the
function in terms of two variables:



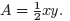
We now need to find a relationship between x and y. We note that
the points (0, y), (3, 5) and (x, 0) must be collinear , so the slope
between (0, y) and (3, 5) must be the same as the slope between (3, 5)
and (x, 0). Thus we get:

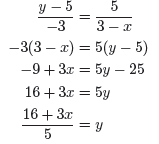
When we substitute this back into our function, we get that

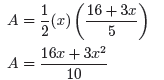
(d) The sum of two numbers is 25. Find the value of the two numbers
that maximizes their product.

i. Express the product P of the two numbers as a function of one
variable.

We start with

P = xy

where x and y are the numbers. We also know that x + y = 25.
If we solve this equation for y, we get that y = 25-x. If we now
substitute this back into the function P, we get:

P = x(25 - x)
P = 25x - x²

ii. This is a quadratic function. Find the maximum of P.

We know that P = 25x - x² is a quadratic with a = -1, so we
know the graph is a downward opening parabola. Therefore, the
maximum of the function will be at the vertex of the parabola.
We know the x-coord of the vertex is

We know from (i) that y = 25 - x, so we know that the two
numbers that maximize P are 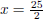and .
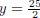The maximum value of the product is 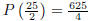.