Math 110 Review Exercises 2
1. Graph the function given by
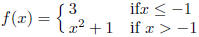
2. Determine the intervals of increase and decrease for
the function
f(x) = x2.
3. Graph a function f satisfying the properties below:
• f is increasing on (-∞, 0).
• f is constant on (0, 2).
• f is decreasing on (2,∞).
• f(-1) = f(3) = 0 and f(1.7) = 1.
4. Sketch the graph of y = lxl. Use it to graph
.
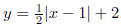5. Find a domain on which the function f(x) = (x-1)2+1
is one-to-one,
and compute f -1 for this restricted function.
6. Find the inverse function to
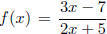, and state the domain
and range for both f and f -1.
7. Graph f(x) = 2x-1, and sketch the graph of the inverse
function on
the same axes.
8. Decide if the functions below are even, odd, or neither.
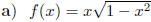
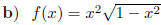
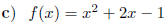
9. Draw a graph of a function that satisfies the
following:
• The domain of f is (-∞,∞).
• The point (1,-3) is a relative minimum of f.
• f is an even function.
• f(0) = 0.
10. Use the graph of f(x) = x3 below to graph the functions:
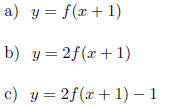
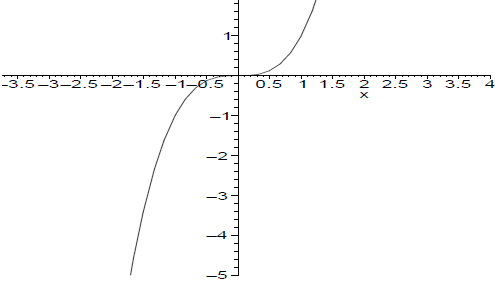
11. Let f(x) = 3x + 4 and g(x) = x2 + x - 1.
Find the following
combinations of these functions.
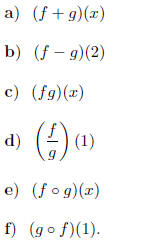
12. Study example 4 on page 291. Use the ideas there to
find the domain
of f o g if f(x) = x2 + 1 and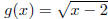 
.
13. Suppose that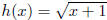 
.
Express h in the form h(x) = (f o g)(x)
for some functions f and g.
14. Let f(x) = x-1. Find f2(x) = (f o f)(x) and f3(x) = (f
o f o f)(x).
Use your answers to guess a formula for fn(x), the n’th iterate of f.
15. For the pairs of functions below, compute f o g and g
o f. Also give
the domain for each function.
16. Use the graph of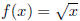 
below to graph the functions:
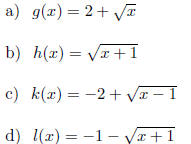
17. Use the graph of f(x) = x2 below to graph the functions:
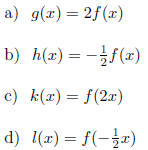
18. Use the graph of f(x) = lxl below to graph the functions:
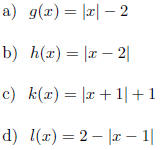
19. Use the graph of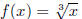 
below to graph the functions:
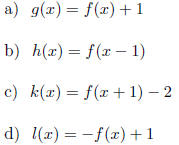
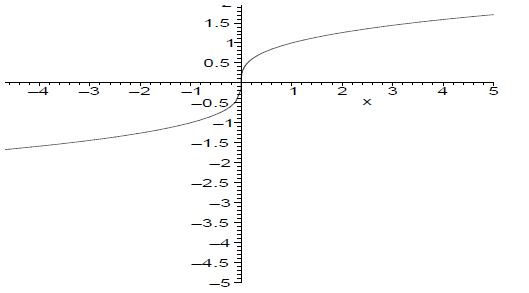
20. By making a sequence of transformations, determine how
the graph
of the function which faces down is related to the graph facing up.
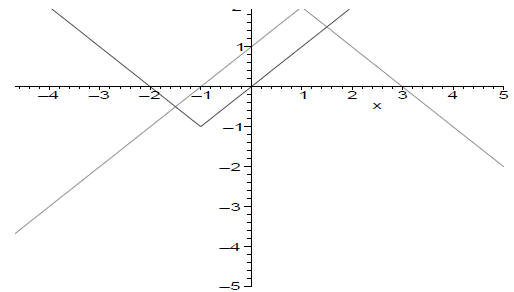
21. Complete the square to find the standard form for the
quadratic
function f(x) = x2 - 4x + 1.
22. Use the vertex formula to find the standard form for the quadratic
function f(x) = -x2 + 5x - 1.
23. Among all pairs of numbers whose sum is 12, find the numbers which
give a maximum product. What is the maximum product?
24. Find the point on the graph of y = x - 3 which is closest to the
point (1,-2).
25. A rancher uses 500 yards of fencing to build a rectangular corral.
What is the largest area that the corral can have?
26. Use the leading coefficient test to determine the left and right hand
behaviour of the function f(x) = -x5 + 3x2 + 1.
27. Use grouping to help find the real zeros of the polynomial function
f(x) = x3 + 2x2 - x - 2. Then graph the function, using
the leading
coefficient to determine the left and right hand behaviour of the function.
28. Use long division to divide f(x) = x4-3x3+x-1 by g(x)
= x2-x+1.
29. Use synthetic division to divide f(x) = x4 - 3x2 + x -
1 by x + 2.
30. Use the remainder theorem to find f(2) if f(x) = x4 - 3x3
+ 2x2 -
6x + 1.
31. Use the factor theorem to determine whether x - 1 is a factor of
f(x) = x5 - 3x3 + x + 1.
32. Find the quotient and the remainder of f(x) = x4 - 3x + 1 divided
by x - 3.
33. Use synthetic division, and the fact that -3 is a root of f(x) =
x3 + 4x2 + x - 6 to express f(x) as a product of 3 linear
factors.