Bases Other than e and Applications
Objective: Define exponential functions that have bases other than e.
Differentiate and integrate exponential functions that have
bases other than e. Use exponential functions to model
compound interest and exponential growth.
Definition of Exponential Function to Base a
If a is a positive real number (a≠1) and x is any real
number, then the exponential function to the base a is
denoted by ax and is defined by
ax = e(lna)x
If a = 1, then y = 1x = 1 is a constant function.
These functions obey the usual laws of exponents
Definition of Logarithmic Function to Base a
If a is a positive real number (a≠1) and x is any
positive
real number, then the logarithmic function to the base
a is denoted by logax and is defined as
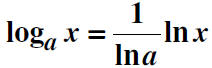
These functions obey the usual laws of logarithms
Differentiation and Integration
To differentiate exponential and logarithmic functions to
other bases you have three options
1. use def’n of ax and logax and differentiate using rules
for natural exponential and log functions
2. use logarithmic differentiation
3. use the following differentiation rules for bases other
than e.
Derivatives for Bases other than e
Let a be a positive real number (a≠1) and let u be a
differentiable function of x.
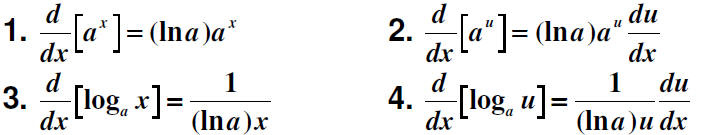
Ex: Find the derivative of each function
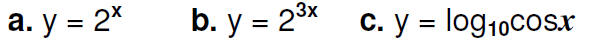
Ex: Find 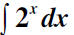
Previously the power rule required n to be a rational
number. However, now the rule can be extended to cover
any real value number.
The Power Rule for Real Exponents
Let n be any real number and let u be a differentiable
function of x.
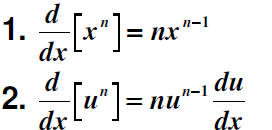
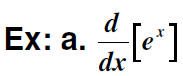
b. Differentiate 


