Study Guide for Algebra
4.1 Simplifying rational expressions
•  where b ≠ 0
where b ≠ 0
• 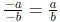 where b ≠ 0
where b ≠ 0
• 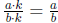 where b, k ≠ 0
where b, k ≠ 0
• Factoring:
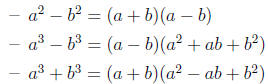
4.2 Multiplying/Dividing rational expressions
• 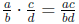 where b, d ≠ 0
where b, d ≠ 0
• 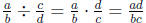 where b, c, d ≠ 0
where b, c, d ≠ 0
4.3 Adding/Subtracting rational expressions
•  where b ≠ 0
where b ≠ 0
• 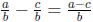 where b ≠ 0
where b ≠ 0
4.4 More rational expressions/complex fractions
• Combining rational expressions:
1. Find LCD
2. Multiply to get equivalent fractions with the same denominator
3. Combine numerators
4. Reduce, if necessary
• Complex fractions:
1. Find LCD of all fractions
2. Multiply numerator and denominator by LCD
3. Simplify
4.6 Fractional equations
• Solving fractional equations:
1. Find LCD
2. Multiply both sides by LCD
3. Solve for variable
4.7 More fractional equations/Applications
• Useful equations:
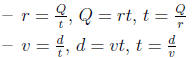
5.1 Using integers as exponents
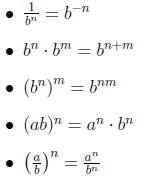
5.2 Roots and radicals
• Properties:
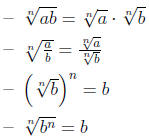
• Simplest radical form:
– Radicant has to be positive and as small as possible
– No fractions in the radicant
– No roots in the denominator
5.3 Combining/simplifying radicals with variables
• You can only add/subtract fractions if the radicant is the same
• Simplify, if necessary!
• Variables: Take out as many multiples as possible
5.4 Products/Quotients involving Radicals
• Combine radicals and simplify
5.5 Equations involving radicals
• Solving equations with radicals:
1. Isolate the root on one side
2. Square both sides
3. Solve for the variable
4. ALWAYS CHECK YOUR ANSWER!
• If there are multiple roots, you might have to repeat the process of
isolating and squaring
5.6 Merging exponents and roots
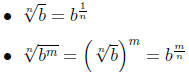
6.1 Complex numbers
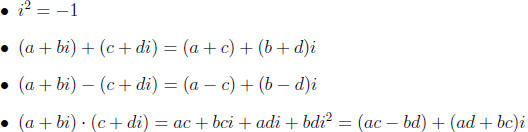
the conjugate of a + bi is a − bi
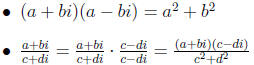
6.2 Quadratic equations
• Factor and solve
6.3 Completing the square

• Completing the square:
1. Make sure there is no factor in front of the square term
2. Divide the coefficient in front of the x-term by 2 and square this
number
3. Add this number and immediately subtract
4. Combine and solve
6.4 Quadratic Formula
• The solutions for the equation ax2 + bx + c = 0 are
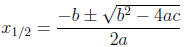
• Discriminant: D = b2 − 4ac
– D > 0: two distinct real solutions
– D = 0: one real solution
– D < 0: two distinct complex solutions
• the sum of the solutions is 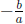
• the product of the solutions is 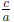
6.5 More quadratic equations/Word problems
• Which method to use:
– all coefficients small: try factoring, then quadratic formula
– b small, c large: complete the square
– all large: try factoring, complete the square
6.6 Quadratic/Nonlinear inequalities
1. Make sure that the right is 0
2. Find critical points: where the left side is either 0 or undefined
3. Graph critical points on the number line
4. Pick test points and determine whether they satisfy the inequalit
8.1 Graphing parabolas
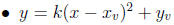
–  is the vertex
is the vertex
– k > 0: concave up
– k < 0: concave down
– |k| > 1: narrower
– |k| < 1: wider
8.2 Parabolas/Circles
• complete the square to bring parabola into standard form
• circle: 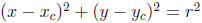 where
where
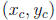 is the center and r
the
is the center and r
the
radius
8.3 Ellipses
• standard form: 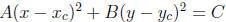 where A,B,C > 0
where A,B,C > 0
• 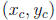 is the center of the ellipse
is the center of the ellipse
• extension in x-direction is 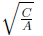
• extension in y-direction is 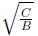
8.4 Hyperbolas
• standard form: 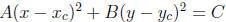 where A,B,C > 0 where
where A,B,C > 0 where
C > 0 and A, B have different signs
• 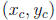 is the center of the hyperbola
is the center of the hyperbola
• finding asymptotes:
1. find the slope: 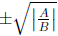
2. use point-slope with the slope and center: 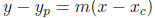
• determine whether it is up/down (B > 0) or left/right (A > 0)
• Determine distance of the vertices from center:
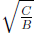 or
or 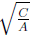
10.1 Systems of two linear equations in two variables
• Substitution:
1. Solve one equations for one variable
2. Substitute into the OTHER equation
3. Solve, then solve for the other variable as well
• Graphing approach:
– different slopes: system consistend, one solution
– same slope, different y-intercepts: inconsistent, no solution
– same slope and y-intercept: dependent, infinitely many solutions
10.2 Elimination-by-Addition Method
1. Make sure that the coefficients for one variable are the same in both
equations with different signs
2. Add equations so that one variable disappears
3. Solve, then solve for the other variable as well


