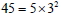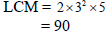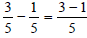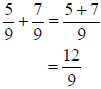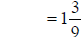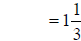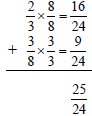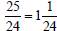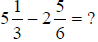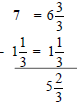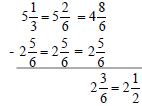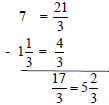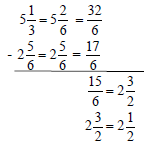Fraction Competency Packet
| Least Common Multiple (LCM) Used to find the Least Common Denominator (LCD) Example: Find the LCM of 30 and 45 Note: There are four common methods; DO NOT mix the steps of the methods! |
||||||
Method 1
|
||||||
Method 2
|
||||||
Method 3
|
||||||
Method 4
|
In each exercise, find the LCM of the given numbers.
1) 4 and 18
2) 16 and 40
3) 20 and 28
4) 5 and 8
5) 12 and 18
6) 12 and 16
7) 50 and 75
8) 24 and 30
9) 36 and 45
10) 8 and 20
11) 16 and 20
12) 28, 35, and 21
| Addition and Subtraction of Fractions with the Same Denominator To add or subtract fractions, the denominators MUST be the same. |
||||||
Example 1: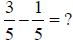
|
||||||
Example 2: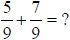
|
Add or Subtract as indicated.
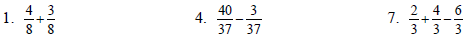
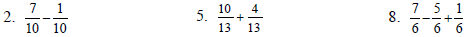

| Addition and Subtraction of Fractions with Different Denominators Remember: In order to add or subtract fractions, the denominators MUST be the same. Example: 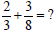
|
Add or Subtract:
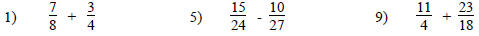
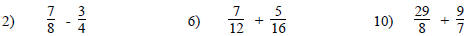

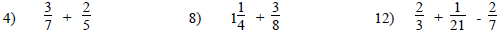
Subtraction of Fractions with
Borrowing
Note: There are two common methods; DO NOT mix the steps of the methods! |
|||
|
Method 1 Example 1
|
Subtraction with Borrowing | ||
|
Write problem vertically Cannot subtract fraction from whole without finding common denominator. |
|||
Borrow one whole from 7 and express as
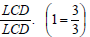 |
|||
| Subtract numerators and whole numbers. | |||
|
Example 2
|
|||
|
Write problem vertically and find LCD Cannot subtract 5 from 2. |
|||
Borrow one whole from 5,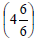 and add and add
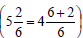 |
|||
|
Subtract numerators and whole numbers; reduce as needed. |
|||
|
Method 2 Example 1:
|
Subtraction Using Improper Fractions Write the problem vertically. |
||
|
Convert the whole numbers and mixed numbers to improper fractions using the LCD. |
|||
Subtract
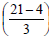 and convert improper fraction to and convert improper fraction tomixed number. |
|||
|
Example 2:
|
Write problem vertically and find the LCD. | ||
| Change the mixed numbers to improper fractions. | |||
|
Subtract the numerators. Convert to a mixed number. |
|||
| Reduce. | |||



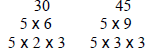
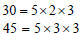 or
or