Inverse Functions
Section 7.1: Inverse Functions
Definition of a One-to-One Function
A function f is one-to-one if no two input values yield the same output. That
is, for
all x, y in the domain of f we have
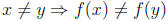
Checking Whether a Function is One-to-One
Horizontal Line Test: If no horizontal line intersects the graph of a function
in more
than one point, then the function is one-to-one.
A function that is always increasing or decreasing is one-to-one. This happens
when
the derivative of a function is always positive or negative.
Definition of Inverse Function:
If f is a one-to-one function with domain A and range B, then the inverse of f,
denoted f −1, is a function with domain B and range A defined by
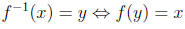
Finding the inverse of a function:
1. Write y = f (x)
2. Solve for x in terms of y.
3. Switch the x and y in the resulting equation to obtain the inverse.
Finding (f −1)'(a) without finding f −1:
Use the formula
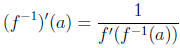
Note: You must be able to find f −1(a), usually by inspection.
Section 7.2: Exponential Functions
Definition of Exponential Function:
An exponential function is of the form
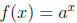
where a is a positive constant.
Properties of Exponential Functions:
If a > 0 and a ≠ 1, then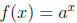
is a continuous function with domain R and range
(0,∞). If a, b > 0 then
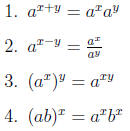
Limits of Exponential Functions:
If a > 1, then 
and
.
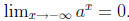If 0 < a < 1, then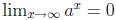 
and
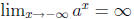
Definition of the Number e:
e is the number such that
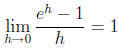
Derivative of the Natural Exponential Function:
The derivative of ex is simply itself:
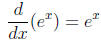
Using the chain rule, we get:
Integrating ex
Use the formula:
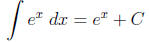
Section 7.3: Logarithmic Functions
Definition of Logarithmic Function:
The inverse function of the exponential function
is called the
logarithmic
function with base a and is written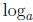 
. The
logarithmic function is defined by
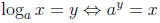
Cancellation Laws for Logarithms:
The following cancellation equations hold for logarithms:
Properties of Logarithms:
If a > 1, the function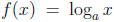 
is a one-to-one,
continuous, and increasing
function with domain (0,∞) and range R. If x, y > 0 and r is a real number then
the following properties hold:
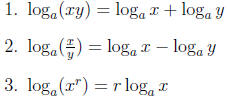
Limits of Logarithms:
If a > 1, then 
and
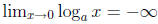
Definition of Natural Logarithm:
The logarithm with base e is called the natural logarithm and is written
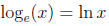
Properties of Natural Logarithm:
The following are defining properties of the natural logarithm
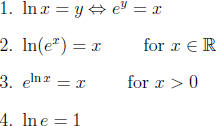
Change of Base Formula:
For any positive number a (a ≠ 1), we have
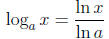
This formula allows us to use a calculator to approximate logarithms of any base.
Section 7.4: Derivatives of Logarithmic Functions
Derivative of the Natural Logarithm
Use the formula
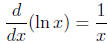
Applying the chain rule gives the formula
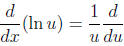
where u is a function in terms of x.
Integration of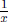 
Integrate by means of the formula
Integration of Tangent
By finding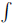 
tan x d x using the integral of
1/x formula, we obtain the following result
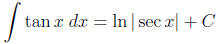
Differentiation Formula for Logarithmic Functions
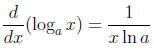
Differentiation Formula for Exponential Functions
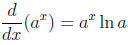
Integration Formula for Exponential Functions
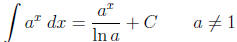
Logarithmic Differentiation
Logarithmic differentiation is useful for taking the derivatives of complicated
functions
containing products, quotients, or exponents.
Procedure for Logarithmic Differentiation:
1. Take the natural logarithm of both sides of an equation y = f (x) and then
simplify using the properties of logarithms.
2. Differentiate both sides of the equation with respect to x being sure to
apply
the chain rule where necessary.
3. Solve the resulting equation for y'.