THE MATHEMATICS OF SYMMETRY
Last modified: October 17, 2008
We define rings and fields, provide basic examples, construct more complex examples, and study the structure of these objects.
Reading: Biggs 22.1-8, 23.1-4
1. List all the axioms for a ring with identity, defined as a set with two
binary
operations, traditionally denoted + and , satisfying a set of axioms that
Biggs summarizes as R1, R2, and R3. Expand R1 into A1-A5, R2 into M1-
M3, and call R3 D. Axioms M5 and M4 are the "extra algebraic properties"
that Biggs mentions at the top of p. 297. A ring which also satisfies M4
(a nonzero factor can be canceled from both sides of an equation) is said
to be a division ring; and a ring which also satisfies M5 is said to be a
commutative ring. A ring that satisfies all eleven axioms with a stronger
version of M4, namely, every nonzero element has a multiplicative inverse,
is said to be a field.
Leave the list of axioms on the board for the next two topics.
2. Show that the integers Z form a commutative division ring with identity,
but not a field. Show that the even integers 2Z satisfy all the axioms except
M3 and thus form a commutative division ring without identity. According
to the definition in Biggs, this is not a ring. Most authors would disagree,
but we will never have occasion to consider rings that without identity and
can therefore safely use the term "ring," as Biggs does, to mean "ring with
identity" (Sections 22.1-22.3.)
3. A number of laws of arithmetic that you have known for a long time are
surprisingly absent from the list of axioms for a ring.
(a) 0a = 0
(b) (−1)a =−a
In fact, they are all easily-proved theorems that follow from the distributive
law and the existence of the multiplicative identity.
(a) By considering (0 + 0)a, prove that 0a = 0 for every element a of a
field. Ask your classmates to prove that a0 = 0 for all a.
(b) Now consider (1+(−1))a and prove that (−1)a =−a. Setting a =−1;
prove that (−1)(−1) = 1. Ask your classmates to prove that a(−1) =
−a for all a.
4. Show that the following examples satisfy the axioms in topic 1. There are
a lot of things to check here, so you may be brief. If any of the proofs of
any of the axioms are unusual, take a little more time there. (Biggs 22.1,
22.3, and 22.4.)
(a) the congruence classes of integers modulo n, denoted Zn, which form
a commutative ring with identity in all cases and a field when n is
prime,
(b) the polynomials with real coefficients, denoted R[x], which form a
commutative ring with identity. Please do not take the time to prove
that multiplication of polynomials is associative!
(c) the n×n matrices with real entries, denoted Mn(R), which form a
ring with identity (and a field in the special case n = 1). (You can
check multiplicative associativity for 2×2 only and simply report that
it works instead of doing it on the board.)
5. Define the more abstract rings of polynomials, F[x], where F is any field.
(In particular, we are interested in the case where F = Zp for a prime
p.) State the Division Algorithm (Biggs Theorem 22.5). Demonstrate the
Division Algorithm using an example from the polynomial ring R[x] (by
which I mean do a long division, different from the example in Biggs).
State the Euclidean Algorithm (Biggs Theorem 22.6). Demonstrate the
Euclidean Algorithm using an example from the polynomial ring Z5[x]
(by
which I mean find the gcd of two smallish but still interesting polynomials
-you will probably have to do a few experiments to find an example which
is simple but still instructive, something like the example in Biggs). State
that these two algorithms work for any polynomial ring F[x] over a field,
but do not present the rather tedious proofs. (Biggs 22.4-22.6.)
6. Consider the equivalence classes of polynomials modulo q(x), for a
specified
polynomial q(x) of degree n. How many such equivalence classes are there
when F = Zp? De ne addition and multiplication on the set of equivalence
classes by [a(x)] + [b(x)] = [a(x) + b(x)] and [a(x)][b(x)] = [a(x)b(x)], and
show that with these definitions, the set of equivalence classes forms another
ring, known as a quotient ring. (Sections 23.1 and 23.3.)
7. In the construction above, show that the quotient ring is in fact a eld
when
q(x) is irreducible. Give examples of irreducible polynomials of degree 2
and 3 in the polynomial rings F[x] when F = Z2,
Z3, and Z5.
Show that
you can check they are irreducible by looking for roots in F (but explain
why this is not the case for higher degree). Include the case p = 3 and
q(x) = x2 + 1, done in Biggs section 23.1.
You can also find examples
of irreducible polynomials at the end of the instructions for the second
programming project. (Sections 22.7-22.8 and 23.3.)
8. For the case where p = 2 and q(x) = x2
+ x + 1, the four elements of the
field are [0],[1], [x], and [x + 1]. Show how to build up the multiplication
table for this field of four elements, F4,
by using the rules that
•All coefficients are in Z2 so that 1 + 1 = 0.
•x2 + x + 1 = 0 so that x2
can always be replaced by x + 1.
9. Review how the field of complex numbers C is built as an extension of the
field of real numbers R by introducing a symbol i that denotes a solution
to the equation i2 + 1 = 0, which has no
solution in the field of real num-
bers. Show how this equation is used to define multiplication in the field of
complex numbers; for example, in calculating (2 + i)(3 + 2i). Explain why
there is really no way to say what is i and what is −i, and contrast this
situation with what happens when you extend the field Q of rational num-
bers by introducing a positive number y (usually denoted
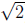) that satisfies
y2−2 = 0.
10. As an alternative but equivalent way of constructing the field F4
as an
extension of the field Z2, introduce a
symbol x that denotes a solution to
the equation x2 + x + 1 = 0, which has no
solution in the field Z2. Show
how this equation satisfied by x is used to define multiplication in the field
F4; for example, in calculating (x + 1)(x).
Explain why there is really no
way to say what is x and what is x + 1.
11. A monic polynomial is one in which the coefficient of the highest power
is
1. Since any non-monic polynomial is simply a constant multiple of some
monic polynomial, in looking for irreducible polynomials we need consider
only monic ones. By counting the number of distinct products of non-zero
monic linear polynomials with coefficients in Zp and the number of non-
zero monic quadratic polynomials with coefficients in Zp, prove that there
exists at least one irreducible monic quadratic polynomial for any prime p
(Section 22.8).
12. For the field F25 with irreducible
polynomial x2 + 3 over F5,
we have the
simple rule x2 = 2 for simplifying
products. Then x = 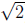. Show that
you can find the inverse of [2+x] by “rationalizing the denominator” (mul-
tiplying b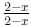y
exactly as you would do if the
coefficients were ordinary
rational numbers. Also show in this case that no power of [x] is equal to
[2 + x]. Use brute force: just compute all the powers up to [x]8.
13. For the field F9 with irreducible
polynomial x2 + 2x + 2 (note { this is not
the same polynomial that Biggs uses in section 23.1) make a table of all the
powers of [x]. In this case [x] is a generator, and you will get every nonzero
element of the field. Show how to use your table to find the inverse of any
nonzero element and to do multiplication by means of addition. This is the
finite case of logarithms. Building a table like this leads to the simplest
way of implementing finite fields in software, as in the second programming
project. (Section 23.4)