Vectors
42.2. A Basis of Vectors (in general)*
The vectors 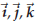 are called the standard basis
vectors. They are an example of what is called a
are called the standard basis
vectors. They are an example of what is called a
“basis”. Here is the definition in the case of space vectors:
Definition 42.1. A triple of space vectors
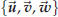 is a basis if every space vector is a basis if every space vector combination of 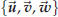 , i.e. , i.e.
|
|
For plane vectors the definition of a basis is almost the same, except
that a basis consists of two vectors rather than three: |
Definition 42.2. A pair of plane vectors
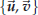 is a basis if every plane
vector is a basis if every plane
vector combination of 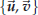 , i.e. , i.e.
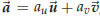 , and if there is only one way to do
so for any given vector , and if there is only one way to do
so for any given vector vector  ). ). |
| 43. Dot Product |
|
Definition 43.1. The “inner product” or “dot product” of two
vectors is given by
|
Note that the dot-product of two vectors is a number!
The dot product of two plane vectors is (predictably) defined by
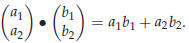
An important property of the dot product is its relation with the length of a vector:

43.1. Algebraic properties of the dot product
The dot product satisfies the following rules,
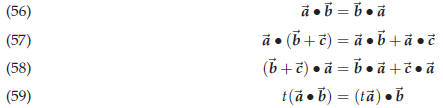
which hold for all vectors and any real number t.
and any real number t.
![]() 43.2 Example.
Simplify
43.2 Example.
Simplify
 .
.
One has
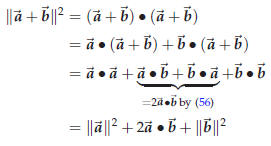
![]()
43.2. The diagonals of a parallelogram
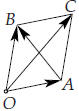 |
Here is an example of how you can use the algebra of the dot product to
prove something in geometry. Suppose you have a parallelogram one of whose vertices is the origin. Label the vertices, starting at the origin and going around counterclockwise, O, A, C and B. Let 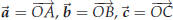 . One has . One has
These vectors correspond to the diagonals OC and
AB
Adding both these equations you get
The squared lengths of the sides are
Together these also add up to
|
43.3. The dot product and the angle between two vectors
Here is the most important interpretation of the dot product:
Theorem 43.4. If the angle between two vectors ![]() and
and
![]() is θ, then one has
is θ, then one has
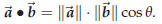
Proof. We need the law of cosines from high-school
trigonometry. Recall that for a triangle OAB with
angle θ at the point O, and with sides OA and OB of lengths a and b, the length
c of the opposing side
AB is given by

In trigonometry this is proved by dropping a perpendicular line from B onto the side OA. The triangle
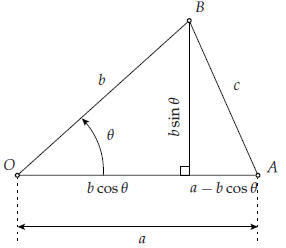
Figure 20. Proof of the law of cosines
OAB gets divided into two right triangles, one of which has AB as hypotenuse.
Pythagoras then
implies
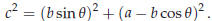
After simplification you get (60).
To prove the theorem you let O be the origin, and then observe that the length
of the side AB is the
length of the vector 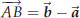 . Here
. Here
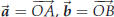 , and hence
, and hence
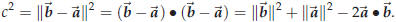
Compare this with (60), keeping in mind that
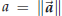 and
and 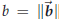 : you
are led to conclude that
: you
are led to conclude that
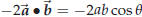 , and thus
, and thus
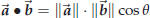 .
.
43.4. Orthogonal projection of one vector onto another
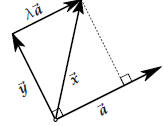
The following construction comes up very often. Let
 be a given vector. Then for any other
be a given vector. Then for any other
vector ![]() there is a
number λ such that
there is a
number λ such that
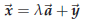
where 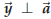 . In other words,
you can write any vector
. In other words,
you can write any vector ![]() as the sum of one vector parallel to
as the sum of one vector parallel to ![]()
and another vector orthogonal to ![]() .
The two vectors
.
The two vectors 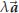 and
and
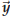 are called the parallel and orthogonal
are called the parallel and orthogonal
components of the vector ![]() (with respect to
(with respect to![]() ), and
sometimes the following notation is used
), and
sometimes the following notation is used

so that
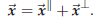
There are moderately simple formulas for
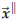 and
and 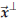 ), but it is better
to remember the following derivation
), but it is better
to remember the following derivation
of these formulas.
Assume that the vectors ![]() and vx are given. Then we look for a number λ such that
and vx are given. Then we look for a number λ such that
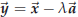 is
is
perpendicular to ![]() .
Recall that
.
Recall that
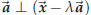 if and only if
if and only if
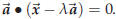
Expand the dot product and you get this equation for λ
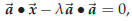
whence

To compute the parallel and orthogonal components of
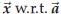 you first compute λ according to (61),
you first compute λ according to (61),
which tells you that the parallel coponent is given by
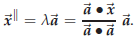
The orthogonal component is then “the rest,” i.e. by
definition 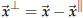 , so
, so
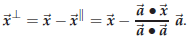
43.5. Defining equations of lines
In § 41 we saw how to generate points on a line given two points on that line by
means of a
“parametrization.” I.e. given points A and B on the line
![]() the point whose
position vector is
the point whose
position vector is 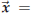
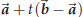 will be on
will be on
![]() for any value of the
“parameter” t
for any value of the
“parameter” t
|
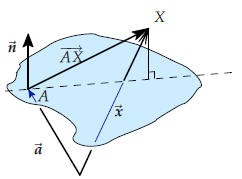
In this section we will use the dot-product to give a different
description of lines in the plane (and planes in three dimensional space.) We will derive an equation for a line. Rather than generating points on the line not. Here is the derivation of the equation of a line in the plane. To produce the equation you need two ingredients: 1. One particular point on the line (let’s call this point A, and write its position vector), 2. a normal vector to the line. Now let X be any point in the plane, and consider the line segment AX. |
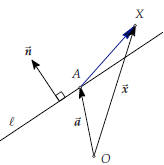
Is X on
|
• Clearly, X will be on the line if and only if AX is
parallel to ![]()
• Since ![]() is
perpendicular to
is
perpendicular to ![]() , the
segment AX and the line
, the
segment AX and the line
![]() will be parallel if and
only if
will be parallel if and
only if
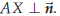
• 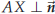 holds if and only if
holds if and only if 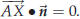
So in the end we see that X lies on the line
![]() if and only if the
following vector equation is satisfied:
if and only if the
following vector equation is satisfied:
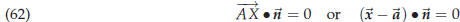
This equation is called a defining equation for the
line
![]() .
.
Any given line has many defining equations. Just by changing the length of the
normal you get a
different equation, which still describes the same line.
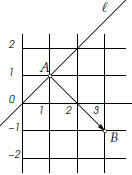 |
to the line segment AB where B is the point (3,−1). Solution. We already know a point on the line, namely A, but we still need a normal vector. The line is required to be perpendicular to AB, so 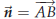 is a normal vector: is a normal vector:
Of course any multiple of
is a normal vector.
If you choose the normal
Both equations
|



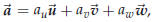
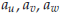 ).
).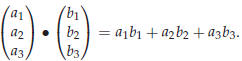
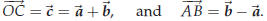
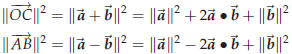
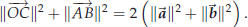
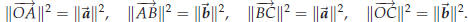
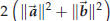 .
.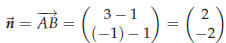
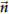 is also a normal vector, for instance
is also a normal vector, for instance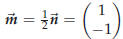
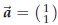 we then get the following equation for
we then get the following equation for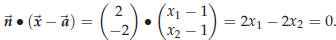
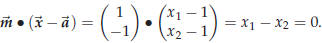
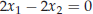 and
and
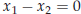 are equivalent
are equivalent