Zeros of the Quadratic

Example 4. Factor 3x² + 34x − 24.

Compare

3x² + 34x − 24 and ax² + bx + c

and note that a = 3, b = 34 and c = −24. List all integer pairs whose product equals
ac = (3)(−24) = −72.

We’ve framed the pair whose sum is the same as b = 34, the coefficient of x in
3x² + 34x − 24. Again, possible shortcuts are possible. If you can “think” of a pair
whose product is ac = −72 and whose sum is b = 34, then it is not necessary to list
any integer pairs. Alternatively, if you come across the needed pair as you are listing
them, then you can halt the process. There is no need to list the remaining pairs if you
have the one you need.

Use the framed pair to express the middle term as a sum, then factor by grouping.

3x² + 34x − 24 = 3x² − 2x + 36x − 24
= x(3x − 2) + 12(3x − 2)
= (x + 12)(3x − 2)

We leave it to the reader to check this result.

Intercepts

The points where the graph of a function crosses the x-axis are called the x-intercepts
of graph of the function. Consider the graph of the quadratic function f in Figure 1.

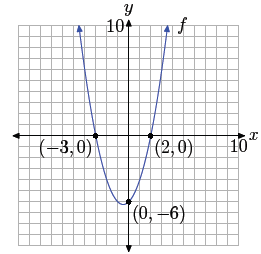
Figure 1. The x- and y-intercepts
are key features of any graph.

Note that the graph of the f crosses the x-axis at (−3, 0) and (2, 0). These are the
x-intercepts of the parabola. Note that the y-coordinate of each x-intercept is zero.

In function notation, the solutions of f(x) = 0 (note the similarity to y = 0) are
the x-coordinates of the points where the graph of f crosses the x-axis. Analyzing the
graph of f in Figure 1, we see that both −3 and 2 are solutions of f(x) = 0.

Thus, the process for finding the x-intercepts is clear.

Let’s look at an example.

Example 5. Find the x-intercepts of the graph of the quadratic function defined
by y = x² + 2x − 48.

To find the x-intercepts, first set y = 0.

0 = x² + 2x − 48

Next, factor the trinomial on the right. Note that the coefficient of x² is 1. We need
only think of two integers whose product equals the constant term −48 and whose sum
equals the coefficient of x, namely 2. The numbers 8 and −6 come to mind, so the
trinomial factors as follows (readers should check this result).

0 = (x + 8)(x − 6)

To complete the solution, we need to use an important property of the real numbers
called the zero product property.

In our case, we have 0 = (x + 8)(x − 6). Therefore, it must be the case that either

x + 8 = 0 or x − 6 = 0.

These equations can be solved independently to produce

x = −8 or x = 6.

Thus, the x-intercepts of the graph of y = x²+2x−48 are located at (−8, 0) and (6, 0).

Let’s look at another example.

Example 6. Find the x-intercepts of the graph of the quadratic function f(x) =
2x² − 7x − 15.

To find the x-intercepts of the graph of the quadratic function f, we begin by setting

f(x) = 0.

Of course, f(x) = 2x² − 7x − 15, so we can substitute to obtain

2x² − 7x − 15 = 0.

We will now use the ac-test to factor the trinomial on the left. Note that ac =
(2)(−15) = −30. List the integer pairs whose products equal −30.

Note that the framed pair sum to the coefficient of x in 2x² − 7x − 15. Use the
framed pair to express the middle term as a sum, then factor by grouping.

2x² − 7x − 15 = 0
2x² + 3x − 10x − 15 = 0
x(2x + 3) − 5(2x + 3) = 0
(x − 5)(2x + 3) = 0

Now we can use the zero product property. Either

x − 5 = 0 or 2x + 3 = 0.

Each of these can be solved independently to obtain

x = 5 or x = −3/2.

Thus, the x-intercepts of the graph of the quadratic function f(x) = 2x² −7x−15 are
located at (−3/2, 0) and (5, 0).

One more definition is in order.

Thus, in the last example, both −3/2 and 5 are zeros of the quadratic function
f(x) = 2x²−7x−15. Note the intimate relationship between the zeros of the quadratic
function and the x-intercepts of the graph. Note that −3/2 is a zero and (−3/2, 0) is
an x-intercept. Similarly, 5 is a zero and (5, 0) is an x-intercept.

The graphing calculator can be used to find the zeros of a function.

Example 8. Use the graphing calculator to find the zeros of the function f(x) =
2x² − 7x − 15.

Enter the function f(x) = 2x² − 7x − 15 into Y1 in the Y= menu; then adjust the
window parameters as shown in Figure 2(b). Push the GRAPH button to produce the
parabola shown in Figure 2(c).

To find a zero of the function, proceed as follows:

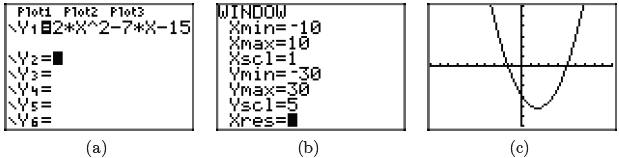
Figure 2. Plotting the quadratic function f(x) = 2x² − 7x − 15.

• Press 2nd TRACE to open the CALCULATE window shown in Figure 3(a). From this
menu, select 2:zero.
• The calculator responds by asking for a “Left bound.” Use the arrow keys to move
the cursor slightly to the left of the leftmost x-intercept, as shown in Figure 3(b).
Press the ENTER key.
• The calculator responds by asking for a “Right bound.” Use the arrow keys to move
the cursor slightly to the right of the leftmost x-intercept, as shown in Figure 3(c).
Press the ENTER key.
• The calculator responds by asking for a “Guess.” You may use the arrow keys to
select a starting x-value any where between the left- and right-bounds you selected
(note that the calculator marks these on the screen in Figure 3(d)). However, the
cursor already lies between these marks, so we typically just hit ENTER at this point.
We suggest you do so also.

Figure 3. Using the zero utility to find an x-intercept.

The calculator responds by marking the x-intercept and reporting its x-value at the
bottom of the screen, as shown in Figure 4(a). This is one of the zeros of the function.
Note that this value of −1.5 agrees nicely with our hand calculated result −3/2 in
Example 6. We followed precisely the same procedure outlined above to find the
second x-intercept shown in Figure 4(b). Note that it also agrees with the hand
calculated solution of Example 6.

In a similar vein, the point where the graph of a function crosses the y-axis is
called the y-intercept of the graph of the function. In Figure 1 the y-intercept of the
parabola is (0,−6). Note that the x-coordinate of this y-intercept is zero.

Thus, the process for finding y-intercepts should be clear.

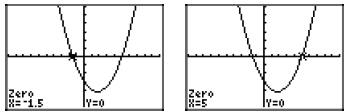
Figure 4. The zeros of f(x)−2x² −7x−15.