Linear Algebra
Read: Boas Ch. 3.
9.1 Properties of and operations with matrices
M × N matrix with elements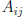 
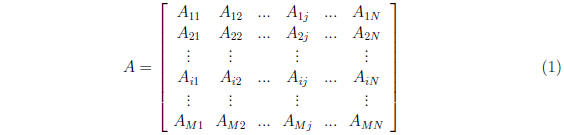
Definitions:
• Matrices are equal if their elements are equal,
.
• 
•
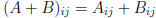
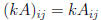for k const.
• 
: Note for multiplication of rectangular
matrices, need
(M × N) · (N × P).
• Matrices need not "commute". AB not nec. equal to BA. [A, B] ≡ AB -BA
is called "commutator of A and B. If [A,B] = 0, A and B commute.
• For square mats. N×N,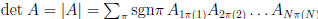 
, where
sum is taken over all permutiations π of the elements {1, ...N }. Each term
in the sum is a product of N elements, each taken from a different row of A
and from a different column of A, and sgn π. Examples:
• detAB = detA · detB but det(A + B) ≠ detA + detB. For
practice with
determinants, see Boas.
• Identity matrix I:
.
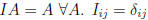• Inverse of a matrix. A · A-1 = A-1A = I.
• Transpose of a matrix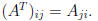 
• Formula for finding inverse:
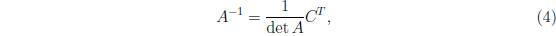
where C is "cofactor matrix". An element
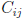is the
determinant of the N -
1 × N - 1 matrix you get when you cross out the row and column (i,j), and
multiply by (-1)i(-1)j . See Boas.
• Adjoint of a matrix. 
is adjoint of
A, has elements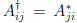 
, i.e. it's
conjugate transpose. Don't worry if you don't know or have forgotten what
conjugate means.
• (AB)T = BTAT
• (AB)-1 = B-1A-1
• "row vector" is 1 × N matrix: [a b c ... n]
• "column vector" is M × 1 matrix:
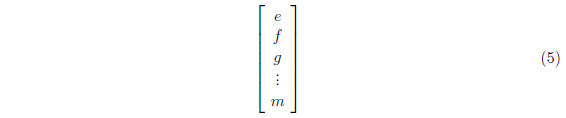
• Matrix is "diagonal" if
.
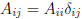• "Trace" of matrix is sum of diagonal elements: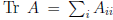
. Trace of
produce is invariant under cyclic permutations (check!):
9.2 Solving linear equations
Ex.
x - y + z = 4
2x + y - z = -1
3x + 2y + 2z = 5
may be written
Symbolically, 
. What we
want is 
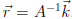. So
we find the determinant
detA = 12, and the cofactor matrix
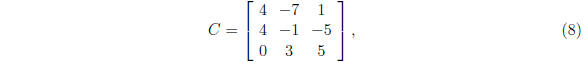
then take the transpose and construct
.
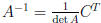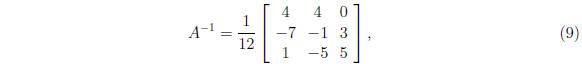
so
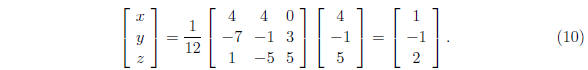
So x = 1, y = -1, z = 2. Alternate method is to use
Cramer's rule (see Boas p.
93):
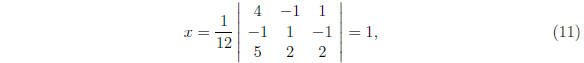
and "similarly" for y and z. Here, the 12 is detA, and the
determinant shown is
that of the matrix of coefficients A with the x coefficients (in this case) replaced
by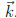 
Q: what happens if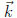 
= 0? Eqs. are homogeneous ) => detA = 0.