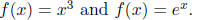Solutions to Homework 4

1. Let 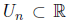be a sequence of open sets containing Q. Prove that 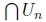contains an irrational number.

Label the rationals q₁, q₂, …, and construct inductively a nested sequence
of closed intervals 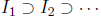with the property that
and 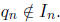Start by taking I₁ an interval containing q₁ and contained in
U₁ (this is made possible by the assumption that U₁ is an open neighbor-
hood of q₁), having constructed I_n, take an open interval J contained in
I_n and not containing q_n, and take for I_n+1 any closed interval contained
in the open set 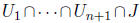which is nonempty since
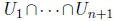
is an open neighborhood of Q, and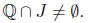

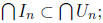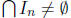It is manifest thatand thatfor a descending chain
of (closed) intervals follows from the completeness axioms of R, alternatively,
from the finite intersection property characterization of compact-
ness. Finally,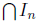contains no rational number, since by construction
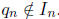The conclusion follows.

Remark. Some of you noted (a special case of the) Baire category
theorem: if X is a complete metric space and U_n a sequence of dense open
subsets, then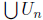is dense. The way this applies is by taking X := R
and the sequence 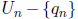of dense open subsets: the intersection of this
sequence must be dense and in particular nonempty, but it contains no
rational number, hence the conclusion. The proof of the general result is
exactly the same.

2. Let f : [0, 1] -> R be a function, and its graph. Prove or
disprove each of the four implications:

f is continuous 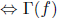is compact 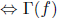is connected:

The only implication that does not hold is that connectedness of the graph
does not imply compactness, as demonstrated by the example of the topologist's
sine curve (whose connectedness was shown on the second homework):

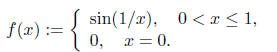
The other three implications hold. Note, first of all, that 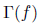is, by
definition, the image of the compact connected interval [0, 1] under the
map 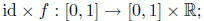this map is continuous if and only if f is.
Since the continuous image of [0, 1] is compact and connected, it follows
that continuity of f implies compactness and connectedness of

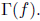
It remains to show that compactness of 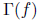implies continuity of f. For
any function 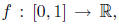the projection map 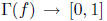onto the
x-axis is a continuous bijection. Recall a very important fact shown in
class: a continuous bijection g : X -> Y from a compact space X is a
homeomorphism, i.e. 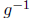: Y -> X is also continuous (Proof: continuity of
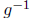means that g is a closed map. To show this, note that compactness of
X implies that every closed subset 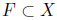is compact, since the continuous
image of a compact space is compact, it follows that g maps any closed
subset of X onto a compact, hence closed, subset of Y , hence g is a closed
map). In our situation, we conclude that compactness of 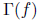implies that
the projection map 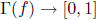onto the x-axis is a homeomorphism, and
this is equivalent to the continuity of f.

3. Prove that if 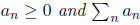converges, then so does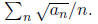

This is an application of the Cauchy-Schwartz inequality: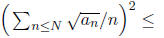

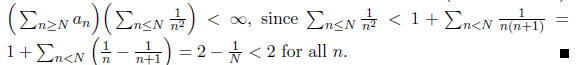
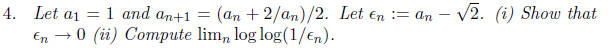
Let 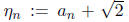(whenever you see 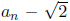and a recurrence with
rational coefficients, always think about 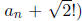and note that the
recurrence 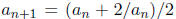may be rewritten a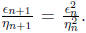s This
shows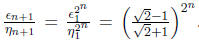Since the right-hand side converges to
0 and 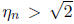for all n, it follows that 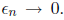Moreover, as it then
follows that 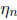is bounded both below and above, the last formula implies

5. Let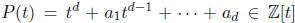 and suppose 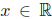satisfies
P(x) = 0. Show that there exists a constant C > 0 such that every rational
number 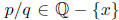satisfies Use this to show that the
number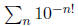 is transcendental.

The idea is to estimate |P(p/q)| from above by the mean value theorem,
and from below by the basic arithmetic estimate 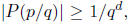which
is simply a reflection of the fact that P(p/q) is a nonzero rational number
of denominator dividing 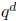. For the upper bound, note that the mean
value theorem provides some 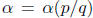between x and p/q such that
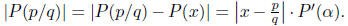Comparing the two bounds,
we may take

This result is called the Liouville inequality, and yields a criterion of
transcendence: if 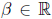is such that for every d there exists a rational
number 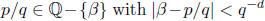then 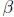is transcendental, such
numbers are called Liouville numbers. An example is the number
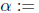
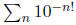and its approximation by the partial sums
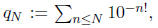
which are rational numbers of denominators 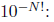since
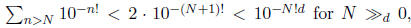it follows that 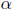is
a Liouville, hence transcendental, number.

Remark. The Liouville inequality is only sharp for d≤2. For d > 2, this
basic result is superseded by a deep theorem of Klaus Roth, which states
that the exponent d can be replaced by any number > 2. More precisely,
for every 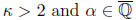algebraic, the set
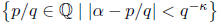
is finite.

6. Prove that the function 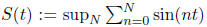is finite for all t ∈ R.
Is it bounded?

There is an exact formula for the sum: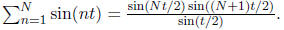
This follows upon successively setting 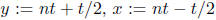in the
formula 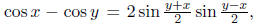and forming the resulting telescoping
sum of identites for n = 1, 2, … ,N. The finiteness of S(t) follows
from this expression: it is bounded above in absolute value by
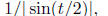
when 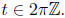and it is identically 0 for 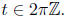It also follows from this
closed form expression that S(t) is not bounded in t, as seen upon taking

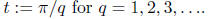
Remark. In fact, it is not difficult to find the exact value of S(t) from
the given closed form evaluation:

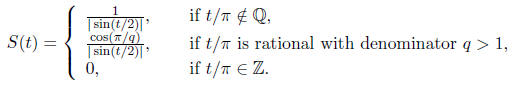
7. Prove that if if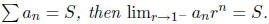

As noted by most of you, the argument appears in Rudin, Theorem 8.2.
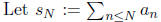be the partial sums, and denote 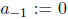. We have
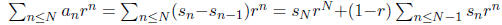showing
for r < 1 that the seri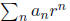es converges to the series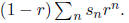
Letting 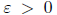arbitrary, there is an M > 0 such that n > M yields

the right hand-side is 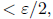and the inequality become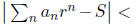
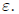Letting proves the required limit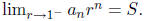

8. Suppose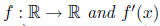 is continuous. Prove that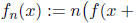
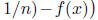converges to f'(x) uniformly on compact intervals [a, b]. Give
an example where the convergence is not uniform on R.

On a compact metric space, a continuous function is uniformly continuous,
thus f' converges uniformly on compact intervals, and hence, for a given
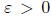, there exists a 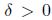such that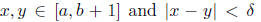
imply 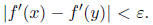For the mean value theorem implies
the existence of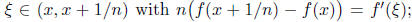 for
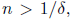this 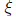satisfies 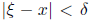, and the uniform continuity implies
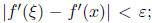that is, 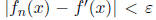for all 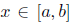and all
This shows the uniform convergence of 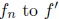on the compact
intervals [a, b].

The convergence need not be uniform on R, the simplest examples are