Circle Conjectures

Lab Summary:
This lab will deal with certain properties of circles. In particular, eight
conjectures will be covered in this lab. As each problem of the lab is completed, the
student should discover certain properties that hold for circles. These properties relate to
tangents lines, inscribed angles, and chords of circles. Upon completion if this lab, the
student should be familiar with all these concepts.

The lesson plan I have implemented involves conjectures of circles. These
conjectures are certain properties on circles that the students will discover through
working with the lab. Included in this lesson plan is:

• A statement of the objectives this lesson will cover, that is, the conjectures to be
discovered by the students. Each conjecture is defined and a diagram of each is
provided. This is the knowledge the students are to have learned after lesson is
complete. The teacher can use this to review the conjectures once the students
have completed the labs to ensure that the students have a firm grasp of the
material. This can also be used as a guide when grading the labs.

• A list of definitions needed in order to complete the lab. These definitions are
meant to be a review of material the student should have seen already. If needed,
the teacher may want to briefly go over each of these terms to ensure that the
students have a firm grasp on this material before starting the lab. The teacher
could also provide each student with a copy of the definitions to be used as a
reference when working on the lab.

• A lab in which the students will explore through Cabri the conjectures to be
covered in this lesson. The lab will help the students to discover for themselves
each conjecture that is to be covered. By completing each lab problem, the
student will learn the conjecture covered by that problem. The lab is a lesson plan
in and of itself, in that, in order to complete the lab, the student must discover
each conjecture. Therefore, it is up to the teacher to decide how much review is
needed before starting the lab, and how much explanation is needed after the lab
is completed to ensure the concepts have been grasped. Two extension questions
are also provided in order to test and challenge what the students have learned
from the lab. Evaluating their lab work will provide an evaluation of the students’
understanding of the material. Successful completion of the lab should result in
the students having a firm grasp of the material.

Key Words:
Circles, tangents, radius, inscribed, perpendicular, chords, tangent segments

Background knowledge:
This lesson will concentrate on certain properties found in circles. The lesson is
implemented through a lab in which the student will discover each property through
experimentation using Cabri. Specifically, the conjectures covered will be:

• Tangent Conjecture I: Any tangent line to a circle is perpendicular to the
radius drawn to the point of tangency.

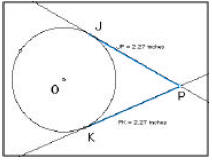
• Tangent Conjecture II: Tangent segments to a circle from a point outside
the circle are equal in length.

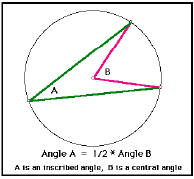
• Inscribed Angles Conjecture I: In a circle, the measure of an inscribed
angle is half the measure of the central angle with the same intercepted
arc.

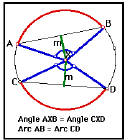
• Inscribed Angles Conjecture II: In a circle, two inscribed angles with the
same intercepted arc are congruent.

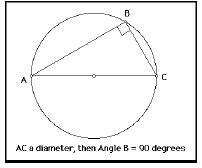
• Inscribed Angles Conjecture III: Any angle inscribed in a semi-circle is
a right angle.

• Congruent Chords Conjecture: If two chords are congruent, then the
following properties hold:
1. They determine central angles that are equal in measurement.
2. Their intercepted arcs are congruent. Also, the chords are equal
distance from the center.

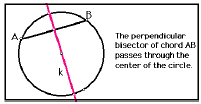
• Perpendicular Bisector of a Chord Conjecture: The perpendicular
bisector of a chord in a circle passes through the center of the circle.

Learning Objectives:
1. Students will discover the eight conjectures covered in background knowledge.

Materials:
Geometry software
Worksheets

Procedures:
Each of these conjectures is covered as a separate problem in the
lab that follows. The student should be able to discover these conjectures themselves by
working out the problems using Cabri. Two extension questions are given which
challenge the student to put to use certain conjectures discovered earlier in order to come
up with a solution.

Extension I requires students to use the perpendicular bisector of a chord property
in order to find the center of any given circle or arc. To do this, the student should
construct two chords in the given circle or arc and bisect each with a perpendicular line.
Where the two perpendicular lines intersect is the center of the circle.

Extension II requires students to use the method found in Extension I to, given
any arc, find the circumference of the circle the arc is a part of. To do this student should
find the center of the circle using the method discovered in Extension I. Once the center
is found, construct a radius and measure it. Use this measurement to find the
circumference of the circle.

Assessment:
Completed worksheets

Circle Conjectures
Activity One: Tangent and Radii

Team members’ names: __________________________________________________
File name: _____________________________________________________________

Goal: Investigate the angle formed by the tangent and the radius of a circle.
a. Construct a circle A with radius . [use circle tool/segment tool]

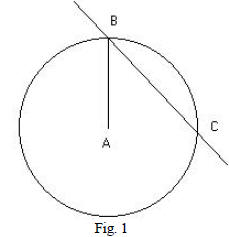
b. Construct a point, C on the circle and draw a secant that runs
through B and C (see Fig. 1). [use point/line tool]

c. Measure the angle ∠ABC that is formed. [use angle tool]

d. Now grab and move point C around the circle until the line suur is
tangent to the circle. What is the measurement of angle ∠ABC now?

What conjecture can you make about a tangent and a radius to the point of
tangency?

e. Use this conjecture to construct a tangent line to a circle at a given
point P.

Circle Conjectures
Activity Two: Tangent Segments

Team members’ names: __________________________________________________
File name: _____________________________________________________________

Goal: Investigate the relationship between tangent segments.
a. Construct a circle A with radius 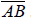[use circle and segment tools]

b. Construct a tangent line, t through B. [use perpendicular line tool]

c. Construct another radius 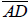and a tangent line, s through C(see Fig2).
[use point, segment, and line tools]

d. Construct and label the point where lines t and s intersect as point D.
[use intersection points and label tool]

e. Measure the tangent segments and 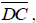  what relationship exists?
[use distance tool]

f. Grab and move point B around the circle. What happens to the segment
measures of 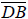and

What conjecture can you make about tangent segments from the same exterior
point?

Circle Conjectures
Activity Three: Central and Inscribed angles

Team members’ names: __________________________________________________
File name: _____________________________________________________________

Goal: Investigate the relationship between inscribed and central angles.
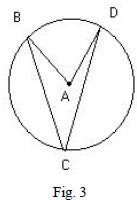
a. Construct a circle A.
b. Construct an inscribed angle ∠BCD.
c. Construct a central angle ∠BAD (see Fig. 3).
d. Measure both angles and compare.
e. Construct diameter
f. Drag point B around the arc DBE. What happens to the angles
measures?

g. What conjecture can you say exists between central and inscribed
angles that share the same intercepted arc?

h. Does your conjecture remain if you drag point B pass point E?
Explain why.

Circle Conjectures
Activity Four: Congruent Inscribed Angles

Team members’ names: __________________________________________________
File name: _____________________________________________________________

Goal: Investigate the relationship between congruent inscribed angles.

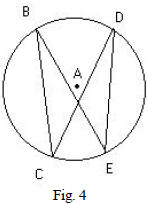
a. Construct a circle A.

b. Construct two inscribed angles, ∠BCD and ∠BED, having them
share the intercepted arc BD (See Fig. 4).

c. Measure the angles and compare.

d. Drag point B around the arc CDE, what happens to the angle
measurements?

e. What conjecture can you say exists between inscribed angles that
share an intercepted arc?

f. What happens when you drag point B pass C to the arc CE?
Explain

Circle Conjectures
ActivityFive: Angles inscribed in a Semi-circle

Team members’ names: __________________________________________________
File name: _____________________________________________________________

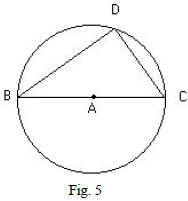
Goal: Investigate angles inscribed in a semi-circle.

a. Draw a circle A with chord BC running through the center of the
circle.

b. Construct an inscribed angle ∠BDC that intercepts the arc BC
(see fig. 5).

c. Measure the angle ∠BDC.

d. Drag point D around the circle, what happens to the angle measure?

e. What conjecture can you say exists for an inscribed angle which
intercepts a half circle?

Circle Conjectures
Activity Six: Congruent Chords

Team members’ names: __________________________________________________
File name: _____________________________________________________________

Goal: Investigate the relationship between congruent chords.

a. Construct a circle A with a chord BC.

b. Construct a new chord DE, which is a reflection of chord BC with
respect to the center of the circle, point A (use the symmetry tool).
Chords DE and BC should be congruent. Measure their lengths to
make sure.

c. Construct central angles ∠BAC and ∠DAE. Measure each of these
angles and compare their values, what relationship exists?

d. Through experimenting, what other conjecture(s) can you find that
exist between congruent chords in a circle? (Hint: examine arcs and
distance from center).

Circle Conjectures
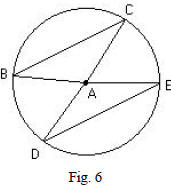
Activity Seven: Radii that Bisect Chords

Team members’ names: __________________________________________________
File name: _____________________________________________________________

Goal: Investigate radii that bisect chords.=

a. Construct circle A with chord BC.

b. Find midpoint of BC and label it M.

d. Construct a radius 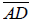through M and measure angle ∠AMC
(see Fig. 7).

d. Drag point B around circle, what happens to the angle measure?

e. What conjecture can you make about a radius that bisects a chord?

Circle Conjectures
Activity Eight: Perpendicular chords

Team members’ names: __________________________________________________
File name: _____________________________________________________________

Goal: Investigate perpendicular chords.

a. Construct a circle A with chord BC.

b. Draw a line from A, perpendicular to chord BC.

c. Find the intersection of line t and chord BC and label it as point P
(Fig. 8).

d. Measure segments 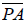and 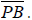What relationship exists?

What conjecture can you make between a chord and a
line perpendicular to that chord through the center of the circle?

Extension 1
Use the conjectures from above to devise a method for finding the center of any
given circle or arc.

Extension 2
Given any arc, can you determine the circumference of the circle it is a part of?
(Hint: use method from Extension 1 to find center of the circle).
Project AMP Dr. Antonio R. Quesada – Director, Project AMP