Sample Math Problems
1. (a) Quadratic equations are equations of the form
………………………………………….
where a, b, and c are real numbers and a ≠ 0.
(b) There are many techniques for solving quadratic equations. List three of
them.
……………………………………………………..
……………………………………………………..
……………………………………………………..
(c) The zeroes of a quadratic function are given by the quadratic formula. What
is the
quadratic formula?
(d) What is the name of the expression under the radical sign in the quadratic
formula?
(e) Solve the following equation by using the quadratic formula. Round answers
to three
decimal places.
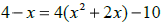
(f) What is the discriminant and how is it related to the x-intercepts of
a quadratic function?
2. An arrow is shot vertically into the air. The height
(in feet) of the arrow after t seconds is
given by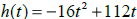 
.
(a) How long before the arrow returns to the ground? Show what you did.
(b) At what time did the arrow reach maximum height? What is the maximum height?
Show or explain what you did.
3. Skill Practice. Answer the following expressions algebraically.
(a) Write the quadratic function in standard form:
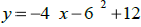
(b) Find the zeroes of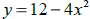 
.
(c) Find the y-intercept of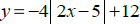 
(d) Write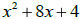 
in vertex form by completing
the square.
(e) i. Simplify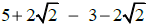 
ii. Simplify
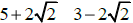
(f) Simplify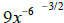 
.
(g) Write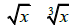 
using exponents. Simplify using properties
of exponents. Write your
result in radical notation.
(h) Simplify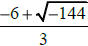 
(i) Expand and simplify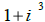 
.
(j) Use your calculator to find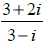 
in fraction
form. ……………………….
Then show how to obtain this result by multiplying both the numerator and the
denominator by the conjugate of the denominator and simplify.
(k) True or False: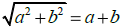 
. Justify your answer.
(l) True or False: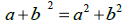 
. Justify your answer.
(m) Simplify the following expressions. Write your final answer without negative
exponents.
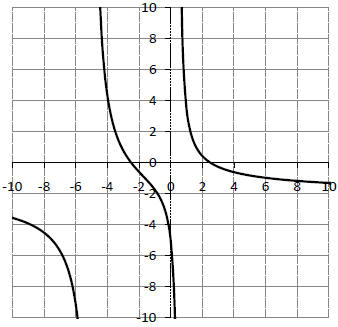
4. Consider the rational function
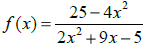
(a) What is the domain of this function?
(b) Write the equation(s) of the any vertical
asymptotes?
(c) Find the y-intercept algebraically.
(d) Find the x-intercepts algebraically.
5. (a) Perform the indicated operations and simplify:
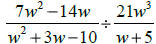
(b) Given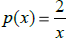
. Evaluate and
simplify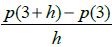 
6. Janet has 35 ounces of liquid that is 20% grape juice.
Suppose she adds x ounces 75% grape
juice.
(a) Write a rational function that represents the concentration of grape juice
in the final
mixture.
(b) How many ounces of liquid containing 75% grape juice must be added to raise
the
concentration to 30% grape juice?
7. The game commission introduces some deer into newly acquired state game
lands. The
population of the herd is given by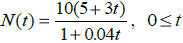 
, where t
is the time in years
since the land was acquired.
(a) What is the y-intercept and what does it mean in this situation?
(b) Find N(12) and explain what it means in this scenario.
(c) How long will it take for the deer population to reach 400? Solve
algebraically and check
with table or graph.
(d) In the long run what would you expect the population to be? Explain.
8. Use algebra to solve each of the following equations.
Remember to check your answers.
Round where appropriate to two decimal places.
