Math Review
Scientific Notation
1. Write the following numbers in scientific notation.
(a) 80,516
(b) 0.0751
(c) 3,520,000
(d) 0.000 000 081
2. Evaluate (without a calculator):
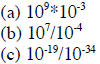
3. Evaluate, in scientific notation (try to do the exponents without a calculator):
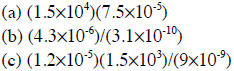
4. Evaluate (without a calculator):
Linear Equations – one variable
5. Solve for x:
Simultaneous Equations
6. Solve for both unknowns:
Hint for (c): Resist the temptation to multiply both
equations by xy to clear the denominators.
Just let u = 1/x and v = 1/y and solve first for u and v, then find x and y.
Polynomials
7. Multiply
(3x2 + 4x – 5) by (2x –1)
Quadratic Equations
8. Solve these quadratic equations by completing the square:
(a) x2 – 4x – 12 = 0
(b) 9x2 – 6x – 1= 0
(c) x + 2x2 = 5/8
(d)(x + 2)(2x – 1) + 3(x +1) = 4
9. Solve these quadratic equations by the general quadratic formula:
(a) 2x2 = 9x – 8
(b) Solve for t:
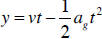
(c) 5x (x + 2) = 2(1 – x)
(d)0.2x2 –1.5x = 3
(e) Solve for x: x2 – 2sx =1 – 2s2
Combining Fractions
10. Evaluate the following combinations of fractions,
bringing the result to a single denominator
in each case and canceling where possible:
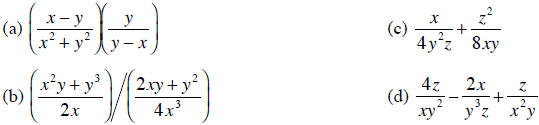
Laws of Exponents
11. Evaluate (without a calculator):
12. Solve for x (without a calculator):
Fractional Exponents
13. Simplify and evaluate (without a calculator):
Exponentials as Functions
14. Combine and simplify (without a calculator):
Logarithms
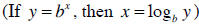
15. Find (without a calculator):
Using Logarithms
16. Given
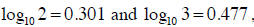find (without a calculator):
17. Use your calculator to evaluate the antilogs (base 10) of the following logarithms:
(a) 5
(b) 3.30103
(c) –0.69897
(d) the sum of (b) and (c)
(e) the difference of (b) and (c)
Right Triangles
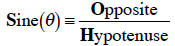
SOHCAHTOA
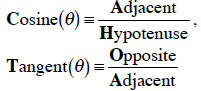
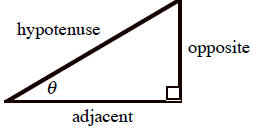
cosecant = 1/sine; secant = 1/cosine; cotangent =
1/tangent
(adjacent)2 + (opposite)2 = (hypotenuse)2
18. Cover up the formulas above. Then, for the triangle
shown here, find
(without a calculator):
(a) sin θ
(b) cos θ
(c) tan θ
(d) csc θ
(e) sec θ
(f) cot θ
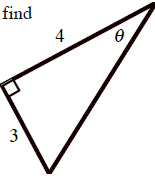
19. For this triangle, find (without a calculator):
(a) sin (90° – θ)
(b) sin θ + cos (90° – θ)
(c) tan θ + cot (90° – θ)
(d) sec θ + csc (90° – θ)
20. Sorry folks. No picture this time. You draw the
triangle. If A is an acute angle and sin A =
7/25, find all the other trigonometric functions of the angle A:
21. For the triangle labeled here, find:
(a) a, if c = 5 and θ = 20°
(b) b, if a = 8 and ø = 40°
(c) c, if b = 6 and θ = 53°
22. For the previous triangle, find all angles and lengths of the sides if:
(a) b = 6, θ = 30°
(b) a = 13, b = 13
(c) c = 10, ø = 30°
(d) c = 12, θ = 45°
(e) c = 1, b =
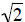
(f) c = 4, b = 4
Geometry
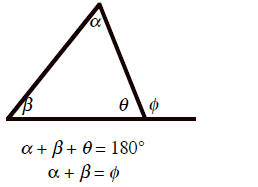
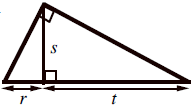
23. Find three similar triangles in the figure shown, and show that s2 = rt
Graphing (Analytic Geometry)
Straight Lines
(y = mx + b, where m = slope and b = y-intercept)
24. Draw a set of xy axes, marked off in equal intervals
between –5 and +5 for both x and y, and
sketch straight lines with the following values of m and b:
(a) m = +2, b = –4
(b) m = –1, b = +4
(c) m = +1/2, b = +1
(d) m = –1, b = –1/3
25. Draw another set of xy axes, marked off as in exercise
24, and draw the following lines, all
passing through the point (2, 1):
(a) m = 0 (c) m = ∞
(b) m = +3/2 (d) m = –2/3
26. Draw another set of xy axes, marked off as before, and
draw lines described by the following
equations:
(a) x + y = 2 (c) x + 2y + 4 = 0
(b) 2x – y + 3 = 0 (d) x – 4 = 0
Parabolas
(x = ay2 + by + c, parabola axis parallel to x axis)
(y = ax2 + bx + c, parabola axis parallel to y axis)
27. Take some squared paper and sketch the following parabolas:
(a) y = –x2
(b) x = 2(y -1)2
(c) y = (x + 2)2