Iterative Solution of Linear Equations

Preface to the existing class notes

At the risk of mixing notation a little I want to discuss the general form of
iterative methods at a general level. We are trying to solve a linear system Ax=b, in a
situation where cost of direct solution (e.g. Gauss elimination) for matrix A is prohibitive.
One approach starts by writing A as the sum of two matrices A=E+ F. With E chosen so
that a linear system in the form Ey=c can be solved easily by direct means. Now we
rearrange the original linear equation to the form:

Ex = b - Fx

Introduce a series of approximations to the solution x starting with an initial guess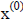
and proceeding to the latest available approximation 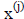. The next approximation is
obtained from the equation:



or



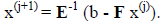
Understand that we never actually generate the inverse of E, just solve the equation for


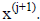
To understand convergence properties of this iteration introduce the residual
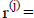
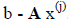. Using this definition and the definition of the iteration, we get the useful
expression:



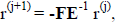
or



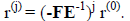
If you know something about linear algebra this tells you that the absolute values of
eigenvalues of FE^-1 should be less than one. This class of iteration scheme includes the
Jacobi, Gauss-Seidel, SOR, and ADI methods.

Another approach is to choose a matrix M such that the product of M^-1 and A is
close to the identity matrix and the solution of an equation like My=c can be obtained
without too much effort. The revised problem can be cast either in the form

M^-1Ax = M^-1b

or

AM^-1 y = b where x = M^-1y

This use of M is referred to as matrix preconditioning. For any given iteration the error



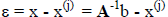
can be approximated as



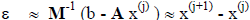
giving a new iteration form of


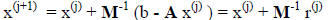
If we start with a guess of 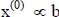, then the iteration yields approximations 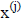which
are combinations of the vectors {b, M^-1Ab, (M^-1A) ² b, … (M^-1A)^k-1 b}. This collection
of vectors is called a Krylov subspace. Krylov solution methods apply the above
iteration philosophy, and modify the coefficients to the vectors in the Krylov subspace to
somehow minimize the residual or error associated with each approximation. This class
of iteration techniques includes the Conjugate Gradient (CG), MINRES, GMRES, QMR,
BiCGSTAB, and a host of related methods. They generally outperform the first class of
iteration by a significant margin.

Summary of Methods

Fluid flow and heat transfer codes generate sparse linear systems in two contexts.
The first is a nearly block tridiagonal system resulting from the equations in 1-D models.
Direct solution methods have worked well for these systems. However, the details of this
approach need reconsideration, if codes are adapted to massively parallel computers. The
second, and more problematic class of sparse matrices are generated by equations
modeling two- and three-dimensional regions. These systems are often only marginally
diagonally dominant, and hence pose a significant challenge to iterative solution
methods. Twenty years ago finding a method that dealt with these equations well was
extremely difficult. Now the biggest problem is sorting through a wide selection of
methods for the problem to find the most appropriate approach.

About fifteen years ago enough experience had been gained with matrix
preconditoning that variants on the Conjugate Gradient method had come into wide
use. Evolution of this methodology has continued with the introduction of several
variations on the basic algorithm. The most popular of these is currently Sonneveld's
conjugate gradient squared (CGS) algorithm . This class of methods has a rate of
convergence that is generally very good, but is not monotonic. Plots of residual versus
iteration count can show oscillations. A stabilized CGS method (CGSTAB)  has been
introduced to mitigate the oscillatory behavior of residuals, but it does not guarantee
monotonically decreasing residuals.

Conjugate Gradient methods currently are losing favor to more general Krylov
subspace methods based largely on the GMRES algorithm . As with conjugate
gradient, this method is based on the construction of a set of basis vectors, and formally
will converge to the exact solution. Rapid convergence in the initial iterations requires
preconditioning of the matrix in both approaches. GMRES type algorithms have the
advantage that residuals decrease monotonically, and that the algorithms are generally
more robust. They have the disadvantage that they must store an additional basis vector
in the Krylov subspace for each iteration. The partial solution to this problem has been to
restart the solution algorithm after some number of iterations.

Providing a recommendation for a "best" solution algorithm is not currently
possible. In fact variability of algorithm performance with machine architecture and
problem type suggests that a "best" algorithm exists only in an average sense. Some
guidance can be obtained from recent publications. Soria and Ruel  provide a
summary of the algorithms mentioned above, and comparisons of GMRES and CGS
using ILU or diagonal preconditioning to results of Broyden , Gauss-Seidel, and
Jacobi iterations. The authors clearly illustrate the value of good preconditioning, and
conclude that more than one solution procedure should be available in a CFD program.
However, they offer no advice on criteria for method selection in such a CFD program.

Chin and Forsyth  provide more detailed information for judging relative
performance of GMRES and CGSTAB with ILU preconditioning. For their problems,
CGSTAB was generally faster than GMRES, but they noted GMRES was not afflicted
with the occasional divide by zero observed in the CGSTAB algorithm. They also note
(but don't document) the sensitivity of conclusions on relative performance of these
methods to the quality of the initial guess for the problem solution.

The interaction between algorithm and machine architecture is always a popular
topic. Recent discussions and references can be found in articles by van Gijzen
(impact of vectorization on GMRES), Sturler and van der Vorst  (GMRES and CG on
distributed memory parallel machines), and Xu et al.  (GMRES for parallel
machines). However, for production codes with a wide user base it is more important to
first select a method that performs well without special vector or parallel considerations.
This helps to minimize non-uniform behavior across platforms. Special vectorized or
parallelized packages should be options that can be activated and checked after initial
code validation on a new installation.

I would recommend several key considerations in choosing a linear system solver.
The starting point, of course, is a set of problems (probably only segments of transients)
that are believed to be representative of the code's workload. Enough solution packages
are publicly available that special programming of algorithms should not be attempted for
initial tests. LASPack  is one resource for testing combinations of preconditioners
and solution algorithms. Once a good (based on robustness and speed) iterative solver
has been selected, the break-even point (in system size) should be determined between
use of the iterative solution and an efficient direct sparse matrix solver. Frequently both
iterative and direct solution packages should be included in a simulation code with an
internal check on the geometry of the mesh to choose between the methods.

If you are willing to wade through lots of Lemmas and Theorems, I recommend
that you read a recent (1997) work by Anne Greenbaum , summarizing the state of
the art at that time. She includes a vary extensive list of references to the literature on
iterative methods.