Precalculus Take Home Quizzes
Take Home Quiz (Logarithmic Functions)
(1) If possible, solve the following equations for t:
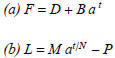
(2) If possible, solve the following equations:
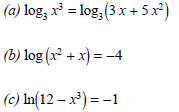
Take Home Quiz (Introducing the Trigonometric Functions)
(1) Suppose θ ≠ 90 ° is an angle of a right triangle, a is the length of the
side adjacent to a, and c is the length of the
hypotenuse. Find the values of the six trigonometric functions for the angle θ
in terms of a and c.
(2) Find the exact values of the trigonometric functions for the acute angle θ given csc θ = 4.
(3) Simplify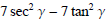 
and
(4) Simplify the expression
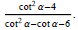
(5) Write the first expression in terms of the second, for any acute angle:
(a) cos θ, cot θ
(b) sin θ, sec θ
(6) For all values θ, verify
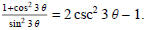
(7) Find the value of the six trigonometric functions given sin θ = 2/3 and cos θ < 0.
(8) The terminal side of angle θ passes through the intersection point of the
given curves. Find the trigonometric
functions of θ, if they exist.
(a) 2 x - y = -10 and 3 x + y = -5
(b) y = x2 - 4 x and y = 4 x - 16.
Take Home Quiz (Trigonometric Angles)
(1) Find the angle that is complementary to θ = 63 °4' 15''.
(2) Express θ = 4 in terms of degrees, minutes, and seconds, to the nearest second.
(3) Express the angle 258 °39' 52'' as a decimal, to the nearest ten-thousandth of a degree.
(4) Show how to construct a unit circle step by step.
(5) Determine whether α < β, α = β, or β < α for α = 80.668 ° and β = 80 °40' 20''. Explain why.
(6) Find the radian measure of the smallest positive angle
that is co-terminal with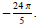 
Take Home Quiz (Trigonometric Graphs)
(1) Sketch the graphs of
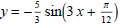and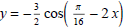 
on separate axes. Label the period, phase shift,
and amplitude. Also label any intercepts and asymptotes.
(2) Sketch the graphs of
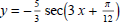and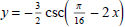 
on separate axes. Label the period, phase shift,
and amplitude. Also label any intercepts and asymptotes.
(3) Sketch the graphs of
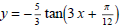and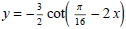 
on separate axes. Label the period, phase shift,
and amplitude. Also label any intercepts and asymptotes.
(4) Sketch the graphs of
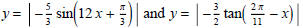on separate axes. Label the period, phase
shift, and amplitude. Also label any intercepts and asymptotes.
(5) Sketch the graphs of
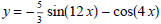and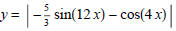 
on separate axes. Label the
period, phase shift, and amplitude. Also label any intercepts and asymptotes.
Take Home Quiz (Trigonometric Identities)
(1) Show the following are not identities:
(a) sin 4 x = 4 sin x
(b) sin(x - y) = sin x - sin y
(c) sin x/2
= 1/2 sin x
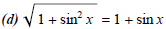
(2) Show that the following are identities:
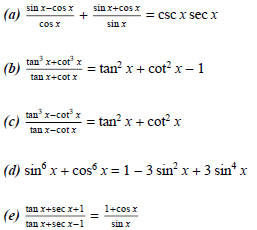
(3) Show that if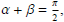 
then cos2
α + cos2 β = 1 and tan α tan β = 1.
Take Home Quiz (Multiple Angle Formulas)
(1) Verify the identities:
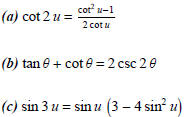
(2) Find all solutions to the equations that are in the interval [0,2 π).
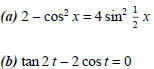
(3) A graph of y = cos 3 x - 3 cos x for -2 π ≤ x ≤ 2 π is shown:
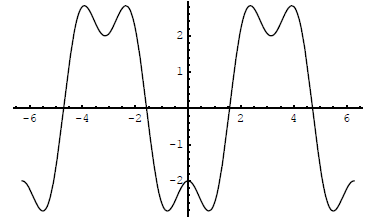
(a) Find the x - intercepts.
(b) The x-coordinates of the 13 turning points on the graph are solutions of sin
3 x - sin x = 0. Find these xcoordinates.
Take Home Quiz (Trigonometric Equations)
(1) Find the solutions of the following equations that are in the interval [0,2π).
(a) cot A + tan A = csc A sec A
(b) sin x + cos x cot x = csc x
(c) sec5 θ = 4 sec θ
(d) 2 tan t csc t + 2 csc t + tan t + 1 = 0
(e) 2 sin v csc v - csc v = 4 sin v - 2
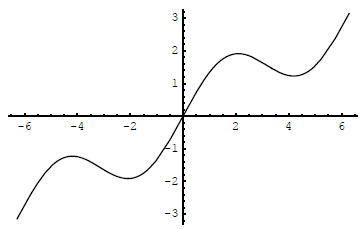
(2) Shown below is the graph of y = 1/2 x + sin x for -2 π
≤ x ≤ 2 π. Using calculus, it can be shown that the
x-coordinates
of the turning points on the graph are solutions to the equation 1/2
+ cos x = 0. Determine the coordinates of these
points.
Take Home Quiz (Solving Triangles)
(1) Solve ∆A BC given the following information.
(a) B = 73 °50', c = 14.0, and a = 87.0.
(b) A = 32.32 °, c = 574.3, and a = 263.6.
(c) A = 42.17 °, a = 5.01 and b = 6.12.
(2) An airplane flies 165 miles from point A in the direction 130 ° and then
travels in the direction 245 ° for 80 miles.
Approximate how far the airplane is from point A?
(3) Given a rectangular box with dimensions 8''×6''×4''. Approximate the angle q
formed by a diagonal of the base
8''×6'' and a diagonal of the 6''×4'' wall.
(4) A baseball diamond has four bases (forming a square) that are 90 feet apart;
the pitcher's mound is 60.5 feet from the
home plate. Approximate the distance from the pitcher's mound to each of the
other three bases.
(5) A rhombus has sides of length 100 centimeters, and the angle at one of the
vertices is 70 °. Approximate the lengths
of the diagonals.