Calculus One: Algebra Review

Outline

1 Section 1.1 - Number Systems
2 Section 1.2 - Coordinates
3 Section 1.3 - Lines and Slopes
4 Section 1.4 - Functions/Graphs
5 Section 1.5 - Combining Functions
6 Section 1.6 - Trigonometric Functions
7 Factoring/Binomial Theorem
8 Solving Equations

Natural Numbers, Integers, Rational Numbers, Real Numbers

The natural numbers, 1, 2, 3, …, are denoted by N
The integers, … ,-3,-2,-1, 0, 1, 2, 3, …, are denoted by
Z. Every natural number is an integer, but not vice versa.
The rational numbers, Q, are defined to be ratios of
integers. Every integer is a rational number, but not vice
versa.
The real numbers, R, can be constructed systematically
from the rational numbers, though this is beyond the scope
of our course. Every rational number is a real number, but
there are real numbers that are not rational (the irrational
numbers).

Sets of numbers

We will use the common notations for sets. For instance,
the set of all x that satisfy some condition P(x) can be
denoted by {x : P(x)}. If S is a set, and x is an element of
S, we write x ∈ S.

We will use the standard interval notation.

You ought to be aware of what sets of real numbers
inequalities such as etc

Triangle Inequality, Approximation

The triangle inequality, one of the fundamental inequalities
in mathematics, is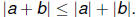

When we write, for example,sqrt(5), we are dealing with the
exact value of this (irrational) number. The number
2.236067977 is not the same number, but is a (rational)
approximation of sqrt(5).

Cartesian Coordinates, Distance, Conics

Every point in the plane (sometimes referred to as R^2), has
a unique representation as an ordered pair (x, y) of real
numbers.

The distance formula: The (Euclidean) distance between
points (a, b) and (c, d) is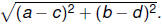

You will need to know how to find the equation of a circle
centered at (h, k) with radius R. Completing the square
plays an essential role here.

You will also need to know the equations of the other
conics - parabolas, ellipses, hyperbolas. (These won’t be
used frequently, but you do need to know them.

Lines

Know the definition of slope.

Perpendicular lines have slopes that are negative
reciprocals of each other.

Parallel lines have equal slopes.

You must know how to find an equation of a line through a
point with a give slope - the point–slope formula is
essential.

Functions

Definition
A function f from a set S to a set T is a rule that assigns at
most one element of T to each element of S. Given x ∈ S, we
denote the element of T that is assigned to x by f (x).

Definition
Given a function f : S -> T, the domain of f is the set of all
x ∈ S that are associated to an element y ∈ T (we say
y = f (x)). The range of f is the set of all such y ∈ T

Types of Functions

We most often define functions algebraically:

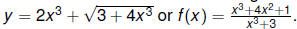However, we will
also consider piecewise–defined functions (see page 34–35)

Definition
The graph of a function f is the set of all points (x, f (x)) such
that x ∈dom(f ). The graph of a function y = f (x) is a curve in
the plane.

Definition
A sequence is a function with domain contained in N. We can
write a sequence by listing its values: f (1), f (2), f (3), ….

Combination of Functions

We’ll often do arithmetic with functions. This should be
routine for everyone.

We’ll also compose functions frequently. Know how to
compute compositions.

We will sometimes use translations of known function
graphs to get graphs of other functions. (see page 49).

Parametric curves - we will address this topic when
needed. Don’t worry about it right now.

Trigonometric Functions

You need to know all six trigonometric functions:
sin x, cos x, tan x, sec x, csc x, cot x and their basic
properties (such as period, whether they’re even or odd
functions, their values at the standard angles, etc.)

Take note of the table of standard values of the trig
functions seen on page 63.

A list of basic trigonometric identities are seen on page 62.
You ought to know these identities, although we won’t use
them extensively.

Basic Factoring

Know how to factor 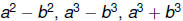, as well as
factoring expressions such as Being able to
factor is an essential skill

Be able to factor quadratics, when such a factorization is
possible

Polynomial Equations

You must be able to solve any quadratic equation

You will also, at times have to solve higher degree
polynomial equations. Generally, at our level, this is done
by factoring or by guessing a root and reducing the
polynomial using division.

Recall that a polynomial of degree n has at most n distinct
real roots.

Binomial Theorem

Let α and β be real numbers and let n be a positive integer.
Then

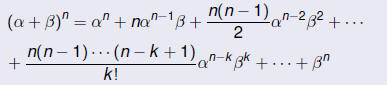
It is good to know this expansion, especially for small n as you
can save a lot of time.