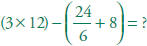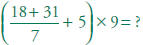The California Mathematics Content Standards
Grade Four Mathematics Content Standards
By the end of grade four, students understand large
numbers and addition, subtraction,
multiplication, and division of whole numbers. They describe and compare simple
fractions
and decimals. They understand the properties of, and the relationships between,
plane geometric figures. They collect, represent, and analyze data to answer
questions.
|
Number Sense
1.0 Students understand the place value of whole numbers and decimals to
two
Solve each of the following problems and
observe the different roles played 1.5 Explain different interpretations of
fractions, for example, parts of a whole, True or false? 1.6 Write tenths and hundredths in decimal and
fraction notations and know the 1.7 Write the fraction represented by a drawing of
parts of a figure; represent a Which number represents the shaded part of the
figure? (Adapted from
True or false?
2.0 Students extend their use and understanding
of whole numbers to the 2.1 Estimate and compute the sum or difference of
whole numbers and positive Solve 55.73 - 48.25 = ? 2.2 Round two-place decimals to one decimal or the
nearest whole number and Solve 17.91 + 2.18 = ?
Solve 619,581 - 23,183 = ?
Solve:
4.0 Students know how to factor small whole
numbers:
List all the distinct prime factors of 210. |
Note: The sample problems illustrate the standards and are written to help clarify them. Some problems are written in a form that can be used directly with students; others will need to be modified, particularly in the primary grades, before they are used with students. The symbol
|
|||||||
|
Algebra and Functions 1.0 Students
use and interpret variables, mathematical symbols, and properties to 1.1 Use letters, boxes, or other symbols to stand
for any number in simple Tanya has read the first 78 pages of a 130-page
book. Give the number of 1. 130 + 78 = ___
Evaluate the two expressions: (28 - 10) - 8 = ___ and 28 - (10 - 8) = ___.
Solve Solve 1.4 Use and interpret formulas (e.g., area =
length × width or A = lw) to answer
|
||||||||
|
Measurement and Geometry 1.0
Students understand perimeter and area:
What is the length of the line segment joining
the points (121, 3) to 3.0 Students demonstrate an understanding of
plane and solid geometric objects
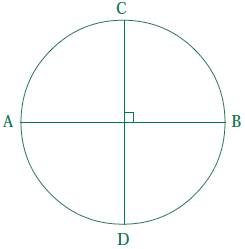
3.5 Know the definitions of a right angle, an
acute angle, and an obtuse angle. 3.8 Know the definition of different
quadrilaterals (e.g., rhombus, square, |
||||||||
|
Statistics, Data Analysis, and Probability
1.0 Students organize, represent, and interpret
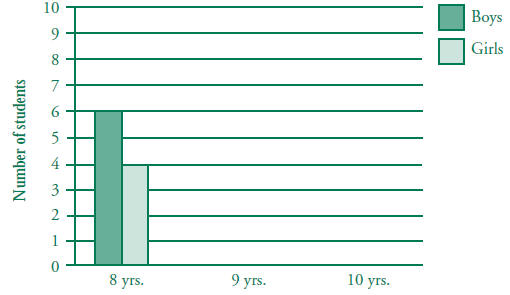
numerical and categorical data and The following table shows the ages of the girls
and boys in a club. Use the
Ages of students 1.1 Formulate survey questions; systematically
collect and represent data on a 2.0 Students make predictions for simple
probability situations: |
||||||||
|
Mathematical Reasoning 1.0 Students make decisions about how to approach problems: 1.1 Analyze problems by identifying relationships, distinguishing relevant from irrelevant information, sequencing and prioritizing information, and observing patterns. 1.2 Determine when and how to break a problem into simpler parts. 2.0 Students use strategies, skills, and concepts in finding solutions: 2.1 Use estimation to verify the reasonableness of calculated results. 2.2 Apply strategies and results from simpler problems to more complex problems. 2.3 Use a variety of methods, such as words, numbers, symbols, charts, graphs, tables, diagrams, and models, to explain mathematical reasoning. 2.4 Express the solution clearly and logically by using the appropriate mathematical notation and terms and clear language; support solutions with evidence in both verbal and symbolic work.
2.5 Indicate the relative advantages of exact and approximate solutions
to |
||||||||



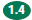 Decide when a
rounded solution is called for and explain why such a
Decide when a
rounded solution is called for and explain why such a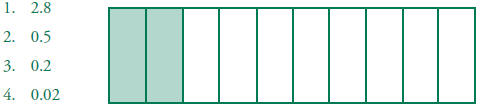
 Use concepts
of negative numbers (e.g., on a number line, in counting, in
Use concepts
of negative numbers (e.g., on a number line, in counting, in Identify on a
number line the relative position of positive fractions, positive
Identify on a
number line the relative position of positive fractions, positive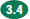 Solve problems
involving division of multidigit numbers by one-digit
Solve problems
involving division of multidigit numbers by one-digit