MATH 3D Homework 3

Section 1.4 Problems

9. Solve the given initial value problem, and determine the interval of existence of the solution.

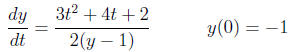
Solution: (15 points) This is a first-order, nonlinear problem, so we use separation of variables:

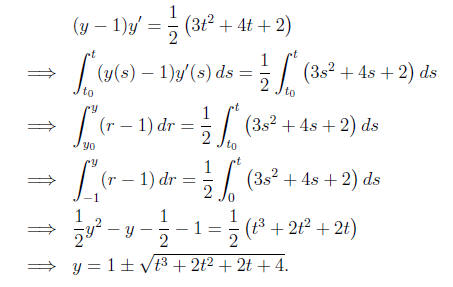
To choose the sign of the root, we note that in the expression above, y(0) can
only be negative if the root is negative. So, the solution is

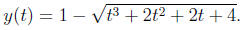
For interval of existence, we seek times t_start < t₀ = 1 < t_tend where the solution
fails, such that the solution never fails on (t_start, t_tend). Well, for this solution,
the only way it can fail is by taking the square root of a negative number, so we
find roots of

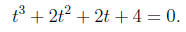
The quickest way to do this is to factor as below:

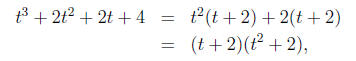
so the only real root is t = -2.

Alternatively, use the rational root theorem to guess a first root: if there's a
rational root, it's one of 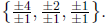Evaluation of these shows that -2 is a
root, and we can factor it (by long division) to

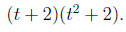The other two roots are complex. So, the solution is valid on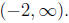

15. Solve the given initial value problem.

Solution: (10 points) This is a first-order, nonlinear problem, so we need
separation of variables. However, the problem is not immediately separable.
(When you have factors lik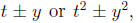e it's a good hint that this is the
case.) We know that we'd eventually like to have f(y)y' = g(t), so dividing both
sides by t is a good start:

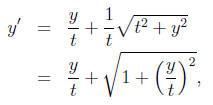
which suggests a new variable v = y/t . Then

To integrate the left side, we use a trig substitution:

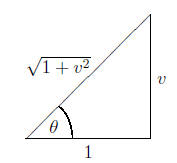
Notice

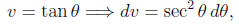
and the integral is

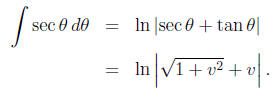
It's easier to plug in the initial condition now:

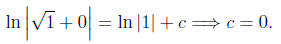
Thus, when we plug in v = y/t and solve for y, we have

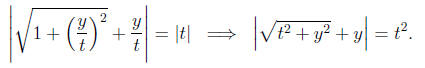
Now, notice that from the original differential equation, if y≥0 and t > 0,

So, if the solution starts at or above 0, it stays above zero. That's the case here,
as y(1) = 0. So,

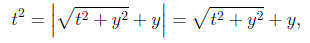
and we can solve for y:

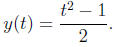
Completeness Points

(4 points) For problems 7, 11, 17, and 19, 1/2 point per moderately-attempted problem, and another 1/2 point per
very-seriously, nearly-properly-solved problem.