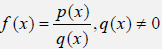Rational Functions
• Find the domain of rational expressions.
• Reduce fractions
| A rational function, f, is the quotient of two
polynomials provided the denominator is not the zero polynomial.
|
Examples:
| The domain of the rational function, f, is the set of all real numbers x for which q(x) ≠ 0. |
Examples: State the domain.
Simplifying Rational Expressions
A rational expression is simplified or reduced to lowest terms or written
in simplest form when
it has no factors (other than 1) common to both its numerator and its
denominator. This
requires us to factor both numerator and denominator and then divide out or
“cancel” factors
common to both the numerator and the denominator.
Examples: Reduce to lowest terms.
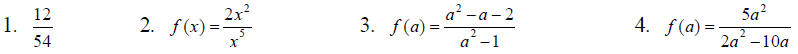
Adding and Subtracting Rational Expressions (8.3):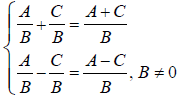
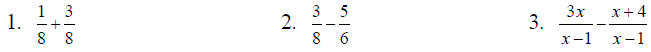
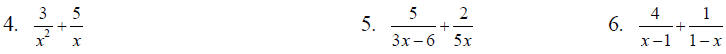
Simplifying Complex Rational Expressions (8.4)
A complex rational expression is a rational
expression whose numerator and/or denominator is a rational
expression.
To simplify a rational expression, put it in
the form of a single-fraction numerator over a single- fraction
denominator. Then take the following steps.
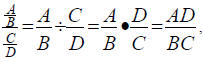where B, C, and D are
nonzero and simplify the result.
Example:
Solving Rational Equations (8.6)
To solve a rational equation:
1. Factor, if possible, the denominators.
2. Find the LCD of the fractions.
3. Multiply both sides by the LCD.
4. Solve the resulting simpler equation.
5. Check that each result satisfies the original equation. Results that do not
satisfy the original equation are
called extraneous solutions.
Note: A solution of an equation is a number, whereas the result of
simplifying a rational
expression is an expression.
Solve the rational equations:
