Polynomials
1 Warm-Ups
1. Consider the cubic equation ax3 + bx2 + cx + d = 0. The roots are
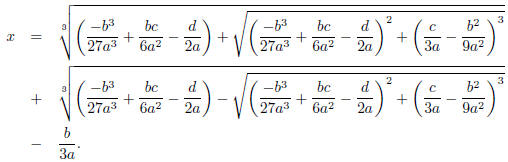
Prove that no such general formula exists for a quintic
equation.
2 Theory
Thanks to Elgin Johnston (1997) for these theorems.
Rational Root Theorem Let 
be a polynomial with
integer coefficients.
Then any rational solution r/s (expressed in lowest terms) must have
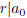and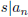 
.
Descartes’s Rule of Signs Let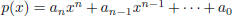 
be a polynomial
with real coefficients.
Then the number of positive roots is equal to N − 2k, where N is the number of
sign changes in the
coefficient list (ignoring zeros), and k is some nonnegative integer.
Eisenstein’s Irreducibility Criterion Let
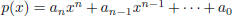be a
polynomial with integer
coefficients and let q be a prime. If q is a factor of each of
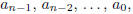but q is not a factor of
an, and q2 is not a factor of a0, then p(x) is irreducible over the rationals.
Einstein’s Theory of Relativity Unfortunately, this topic is beyond the scope of
this program.
Gauss’s Theorem If p(x) has integer coefficients and p(x) can be factored over
the rationals, then p(x)
can be factored over the integers.
Lagrange Interpolation Suppose we want a degree-n polynomial that passes through
a set of n+1 points:
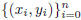. Then the polynomial is:
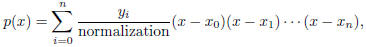
where the i-th “normalization” factor is the product of
all the terms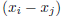 
that have j ≠ i.
3 Problems
Thanks to Elgin Johnston (1997) for most of these problems.
1. (Crux Math., June/July 1978) Show that
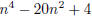is composite when n is
any integer.
Solution: Factor as difference of two squares. Prove that neither factor can be
±1.
2. (St. Petersburg City Math Olympiad 1998/14) Find all polynomials P(x, y) in
two variables such that
for any x and y, P(x + y, y − x) = P(x, y).
Solution: Clearly constant polynomials work. Also, P(x, y) = P(x + y, y − x) =
P(2y,−2x) =
P(16x, 16y). Suppose we have a nontrivial polynomial. Then on the unit circle,
it is bounded because
we can just look at the fixed coefficients. Yet along each ray y = tx, we get a
polynomial whose translate
has infinitely many zeros, so it must be constant. Hence P is constant along all
rays, implying that P
is bounded by its max on the unit circle, hence bounded everywhere. Now suppose
maximum degree
of y is N. Study the polynomial
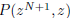. The leading coeff of this is equal
to the leading coeff of
P(x, y) when sorted with respect to x as more important. Since the z-poly is
also bounded everywhere,
it too must be constant, implying that the leading term is a constant.
3. (Putnam, May 1977) Determine all solutions of the system
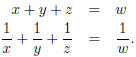
Solution: Given solutions x, y, z, construct 3-degree
polynomial P(t) = (t − x)(t − y)(t − z). Then
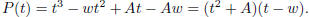In particular, roots are w and a
pair of opposites.
4. (Crux Math., April 1979) Determine the triples of integers (x, y, z)
satisfying the equation
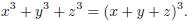
Solution: Move z3 to RHS and factor as x3 ±y3. We get (x+y) = 0 or (y +z)(z +x)
= 0. So two
are opposites.
5. (USSR Olympiad) Prove that the fraction (n3+2n)/(n4+3n2+1) is in lowest terms
for every positive
integer n.
Solution: Use Euclidean algorithm for GCD. (n3 + 2n)n = n4 + 2n2, so difference
to denominator
is n2 + 1. Yet that’s relatively prime to n(n2 + 2).
6. (Po, 2004) Prove that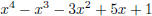 
is irreducible.
Solution: Eisenstein with substitution x → x + 1.
7. (Canadian Olympiad, 1970) Let P(x) be a polynomial with integral
coefficients. Suppose there exist
four distinct integers a, b, c, d with P(a) = P(b) = P(c) = P(d) = 5. Prove that
there is no integer k
with P(k) = 8.
Solution: Drop it down to 4 zeros, and check whether one value can be 3. Factor
as P(x) =
(x − a)(x − b)(x − c)(x − d)R(x); then substitute k. 3 is prime, but we’ll get
at most two ±1 terms
from the (x − α) product.
8. (Monthly, October 1962) Prove that every polynomial over the complex numbers
has a nonzero polynomial
multiple whose exponents are all divisible by 109.
Solution: Factor polynomial as
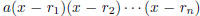. Then the
desired polynomial is
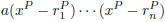, where P = 109. Each factor divides the corresponding factor.
9. (Elgin, MOP 1997) For which n is the polynomial
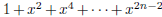divisible by the polynomial
?
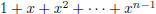Solution: Observe:
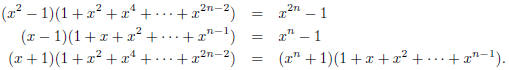
So if the quotient is Q(x), then Q(x)(x + 1) = xn + 1.
This happens iff .1 is a root of xn + 1, which
is iff n is odd.
10. (Czech-Slovak Match, 1998/1) A polynomial P(x) of degree n ≥5 with integer
coefficients and n
distinct integer roots is given. Find all integer roots of P(P(x)) given that 0
is a root of P(x).
Solution: Answer: just the roots of P(x). Proof: write
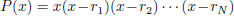. Suppose
we have another integer root r; then
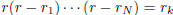for some k.
Since degree is at least 5,
this means that we have
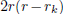dividing rk. Simple analysis shows that r is
between 0 and rk; more
analysis shows that we just need to defuse the case of 2ab | a + b. Assume a ≤b.
Now if a = 1, only
solution is b = 1, but then we already used ±1 in the factors, so we actually
have to have
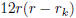
dividing rk, no good. If a > 1, then 2ab > 2b ≥a + b, contradiction.
11. (Hungarian Olympiad, 1899) Let r and s be the roots of
Prove that r3 and s3 are the roots of
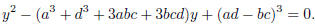
Hint: use Linear Algebra.
Solution: r and s are the eigenvalues of the matrix
The y equation is the characteristic polynomial of the
cube of that matrix.
12. (Hungarian Olympiad, 1981) Show that there is only one natural number n such
that 
is
a perfect square.
Solution: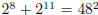 
. So, need to have 2n as difference of squares
.
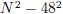Hence (N + 48),
(N − 48) are both powers of 2. Their difference is 96. Difference between two
powers of 2 is of the
form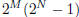 
. Uniquely set to
.
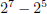13. (MOP 97/9/3) Let 
be a set of n distinct complex
numbers, for some n ≥9, exactly
n − 3 of which are real. Prove that there are at most two quadratic polynomials
f(z) with complex
coefficients such that f(S) = S (that is, f permutes the elements of S).
14. (MOP 97/9/1) Let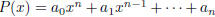 
be a nonzero polynomial with
integer coefficients
such that P(r) = P(s) = 0 for some integers r and s, with 0 < r < s. Prove that
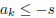for some k.