Polynomial and Rational Functions

Section 2.1 Quadratic Functions
Section Objectives: Students will know how to sketch and analyze graphs of quadratic functions.

Functions already seen:

f (x) = ax + b Linear function

g(x) = c Constant Function

h(x) = x² Squaring Function

I. The Graph of a Quadratic Function

A polynomial function is a function of the form

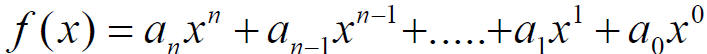
where each a_n is a real number, n is a nonnegative
integer.
Note: that we have already dealt with two forms of this
equation, when n = 0 (constant) and n = 1 (linear). In this
section we focus on n = 2. These are called quadratic
functions and we simplify the notation to be
f (x) = ax² + bx + c, with a ≠ 0 .

Examples are:

Characteristics of a Quadratic Function:
• The Graph of a Quadratic function is “U” shaped
called a Parabola.
• All Parabolas are symmetric with respect to a line
called the axis of symmetry, or simply the axis of the
parabola.
• The point where the axis intersects the parabola is the
Vertex of the parabola.
• If the leading coefficient is positive, the graph
f (x) = ax² + bx + c is a parabola that opens up.
• If the leading coefficient is negative, the graph
f (x) = ax² + bx + c is a parabola that opens down.

Draw the graph of y = ax² and identify the vertex and the axis.

How does the graph change if:
a > 0, 0 < a < 1, & a > 1

II. The Standard Form of a Quadratic Function

The quadratic function f(x) = a(x - h)² + k,
where a ≠ 0 is in standard form.
The graph of f(x) is a parabola with:
• vertical axis x = h
• vertex at (h, k).
• If a > 0, the parabola opens upward
• If a < 0, the parabola opens downward.
Ex: Find the vertex of the following parabola.
(use completing the square)
f (x) = -2x² - 4x +1

Ex: Graph the following quadratic function. (use completing the square)
f (x) = x² - 4x - 2

Ex: Find the standard form of the equation of the
parabola that has vertex at (1, -2) and passes through
the point (3, 6).
Some quadratics are not easy to write in Standard Form
to find the Vertex there is an alternative method we can
use.

For a quadratic of the form f (x) = ax² +bx +c
The Vertex of the Parabola is point

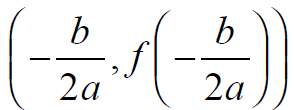
Use this formula to find the vertex of
f (x) = 2x² - 3x +1

Finding the x-intercepts of a Quadratic Function
To find the x-intercepts of the graph of:
f (x) = ax² +bx +c

You must find the zero’s of the function, solve f(x)=0

Remember: a parabola may have zero, one or two xintercepts
Find the Vertex and the x- intercepts and graph
f (x) = -x² + 6x - 8

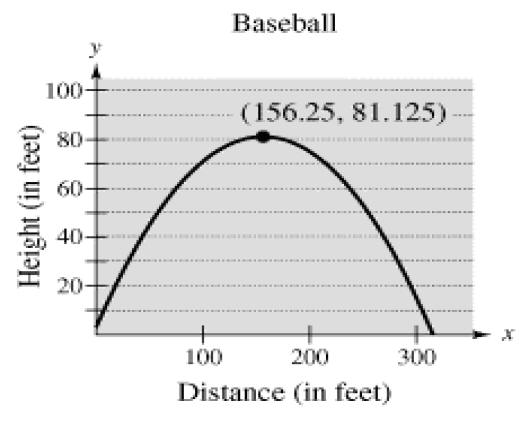
III. Application

Example: Maximum height of a baseball
A Baseball is hit at a point 3 feet above the ground at a
velocity of 100 feet per second and at an angle of 45
degrees with respect to the ground. The path of the ball is
given by the function
f (x) = -.0032x² + x + 3