Integers and Division

Recap
•f(x)∈O(g(x)) if ∃k∈R, ∃c∈R, ∀x∈R, x>k ⇒ 0≤|f(x)|≤c|g(x)|.
•f(x)∈Ω(g(x)) if ∃k∈R, ∃c∈R, ∀x∈R, x>k ⇒ |f(x)| ≥ c |g(x)|.
•f(x)∈θ(g(x)) if f(x)∈O(g(x)) and f(x)∈Ω(g(x)). Equivalently,
•if ∃k∈R, ∃c1,c2∈R, ∀x∈R, x>k ⇒ c1 |g(x)| ≤ |f(x)| ≤ c2 |g(x)|.

ch3.4
Integers and Division

Division
• Def: a (a≠0) divides b if ∃ c such that b = ac.
a | b: a divides b
• 3 | 7? 3 | 12?
• 3 | 0? 0 | 3?
• Theorem: Let a, b, c be integers. Then
a | b, a | c ⇒ a | (b + c).
a | b ⇒ a | bc ∀ c ∈ Z.
a | b, b | c ⇒ a | c.

• Let a, b, c be integers. Then
a | b, a | c ⇒ a | (b + c).

• Let a, b, c be integers. Then
a | b ⇒ a | bc ∀ integer c.

• Let a, b, c be integers. Then
a | b, b | c ⇒ a | c.

• a | b and b | c ⇒ a | (mb + nc) for all
integer m, n.

Division Algorithm
• Theorem: Let a be an integer and d a
positive integer. Then there exist unique q
and r, with 0≤q<r, such that a = dq + r.
• 101 = 7 • 14 + 3
• -11 = 7 • (-2) + 3

Modular Arithmetic
• Def: a, b: integers, m: positive integer, a is
congruent to b modulo m if m | (a - b).
• a ≡ b mod m
• a ≡ b (mod m) iff a % m = b % m.
• 17 ≡ 12 mod 5, 17 % 5 = 2, 12 % 5 = 2
• -3 ≡ 17 mod 10, -3 % 10 = 7, 17 % 10 = 7

• Theorem: Let m be a positive integer.
a ≡ b mod m iff ∃ k such that a = b + km.

More…
• Theorem: Let m be a positive integer. If a ≡
b mod m and c ≡ d mod m, then
a + c ≡ b + d mod m.
ac ≡ bd mod m.

• Prove or Disprove
If ac ≡ bc (mod m), where a, b, c, m ∈ Z
(with m ≥ 2), then a ≡ b (mod m).
a, b, c, d, m ∈ Z, c, d > 0, m ≥ 2,
then a^c ≡ b^d mod m.
a = 2, b = 5, c = 4, d = 1, m = 3

Caesar Cipher
• Alphabet to number: a~0, b~1, … , z~1.
• Encryption: E_K(x) = x + K mod 26.
• Decryption:
• Caesar used K = 3.
• If you don’t know K and you have a secret
text, would you be able to find K? How?

ch 3.5
Primes and GCD

Prime numbers
• Def: A positive integer p is prime if the only
positive factors of p are 1 and p
If there are other factors, it is composite
Note that 1 is not prime!
It’s not composite either – it’s in its own class
• Def: An integer n is composite if and only if
there exists an integer a such that a | n and
1 < a < n

Fundamental theorem of arithmetic
• Every positive integer greater than 1 can be
uniquely written as a prime or as the product of two
or more primes where the prime factors are written
in order of non-decreasing size
• Examples
100 = 2 * 2 * 5 * 5
182 = 2 * 7 * 13
29820 = 2 * 2 * 3 * 5 * 7 * 71

Composite factors
• If n is a composite integer, then n has a prime divisor
less than or equal to the square root of n

Showing a number is prime!
• Show that 113 is prime
• Solution
The only prime factors less than √113 = 10.63 are
2, 3, 5, and 7
Neither of these divide 113 evenly
Thus, by the fundamental theorem of arithmetic,
113 must be prime

Primes are infinite
• Theorem (Euclid): There are infinitely many prime
numbers
(Proof) Proof by contradiction
Assume there are a finite number of primes
List them as follows: p₁, p₂ …, p_n.
Consider the number q = p₁p₂ … p_n + 1
Since we have only finite number of primes and q
is not one of them, pi should divide q for some i.
Obviously p_i| p₁p₂ … p_n.
Recall that a | b, a | c ⇒ a | b + c.
Therefore, pi | (q - p₁p₂ … p_n) = 1. (*)

The prime number theorem
• The radio of the number of primes not exceeding x
and x/ln(x) approaches 1 as x grows without
bound
Rephrased: the number of prime numbers less than x
is approximately x/ln(x)
When x = 2⁵¹², # of primes = 2⁵¹²/512 ∼ 2⁵⁰³

Greatest common divisor
• The greatest common divisor of two integers
a and b is the largest integer d such that
d | a and d | b
Denoted by gcd(a,b)
• Examples
gcd (24, 36) = 12
gcd (17, 22) = 1
gcd (100, 17) = 1

Relative primes
• Two numbers are relatively prime if they
don’t have any common factors (other than
1)
Rephrased: a and b are relatively prime if
gcd (a,b) = 1
• gcd (25, 39) = 1, so 25 and 39 are relatively
prime

Pairwise relative prime
• A set of integers a₁, a₂, … a_n are pairwise relatively
prime if, for all pairs of numbers, they are relatively
prime
Formally: The integers a₁, a₂, … a_n are pairwise relatively
prime if gcd(a_i, a_j) = 1 whenever 1 ≤ i < j ≤ n.
• Example: are 10, 17, and 21 pairwise relatively
prime?
gcd(10,17) = 1, gcd (17, 21) = 1, and gcd (21, 10) = 1
Thus, they are pairwise relatively prime
• Example: are 10, 19, and 24 pairwise relatively
prime?
Since gcd(10,24) ≠ 1, they are not

More on gcd’s
• Given two numbers a and b, rewrite them
as: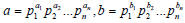
Example: gcd (120, 500)
120 = 2³*3*5 = 2³*3¹*5¹
500 = 2²*5³ = 2²*3⁰*5³
• Then compute the gcd by the following
formula: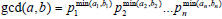
Example: gcd(120,500) = 2^min(3,2)3^min(1,0)5^min(1,3)
= 2²3⁰5¹ = 20

Least common multiple
• The least common multiple of the positive
integers a and b is the smallest positive
integer that is divisible by both a and b.
Denoted by lcm (a, b)

• Example: lcm(10, 25) = 50
• What is lcm (95256, 432)?

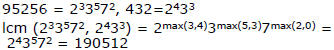
lcm and gcd theorem
• Let a and b be positive integers. Then
a*b = gcd(a,b) * lcm (a, b)

• Example: gcd (10,25) = 5, lcm (10,25) = 50
10*25 = 5*50

• Example: gcd (95256, 432) = 216, lcm (95256,
432) = 190512
95256*432 = 216*190512

Example Proof
• Prove or disprove that n² - 79n + 1601 is
prime, whenever n is a positive integer.
(Disprove)
When n = 1601,
n² - 79n + 1601 = 1601 (1601 - 79 + 1)
• Prove or disprove that p_1p_2…p_n+1 is a
prime, whenever n is a positive integer.
2*3*5*7*11*13+1 = 30031 = 59 * 509