Miscellaneous Math Topics
These a are supplementary notes for week 3. They elaborate
the material
presented in lecture and provide practice problems. Please also read Hagle
chapters 1 and 2.
1 Common Math Notation and Review
Notation for calculus and linear algebra is presented in week 10. This section
presents general mathematical and pre-calculus notation and terms.
1.1 Terms and Definitions
• Axiom: Something we take as given (we do not prove that it is true)
• Constant: A fixed number that does not change
• Denominator: Top part of a fraction
• Numerator: The lower part of a fraction
• Proposition: A rule or formula that we can prove to be true
• Variable: In math, this is something that is unknown or something that
can take finitely or infinitely many values. In statistics it is something
that varies accross observations.
1.2 Symbols and Etc.
1.2.1 Parantheses and Brackets
The curvy brackets {} are used to indicate sets. For example, S={1,2,3} means
that the set S contains the values 1, 2, and 3.
The square brackets [ ] and the parentheses () are used to indicate open
and closed intervals. An open interval does not include its endpoints whereas
a closed interval does include its endpoints. Open intervals use parentheses
and closed intervals use square brackets. For example, the interval (1,5) is the
interval from 1 to 5, exclusive – this means that 1 and 5 are not included in
the
interval. The interval [1,5] is the interval from 1 to 5, inclusive – 1 and 5
are
included in the interval. (1,5] means that 5 is included but 1 is not.
The parentheses are also used to represent points. It should be clear from
context whether (a,b) refers to the open interval from a to b or to the point
(a,b).
Parentheses can also represent multiplication: (2)(4) = 2
* 4 = 8. Paren-
theses indicate that some operation (such as multiplication) is done to the
entire expression within the parentheses as a unit. For example, it is use-
ful when multiplying things with more than one component (polynomials):
(1 + x)(2 + 3x) = 2 + 5x + 3x2.
1.2.2 Infinity
Infinity is represented by ∞ and negative infinity (infinitely small; smaller
than
zero) is represented by -∞.
1.2.3 Inverses
The inverse (reciprocal) of a number n is 1/n. It is often expressed as n
-1. This
is a particular example of an exponent (see below for more about exponents).
Exercises: Notation
1. How do you express the closed interval from negative infinity to two?
2. What is the invserse of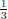 
?
1.3 Variables and Lists
Sometimes we need to express a series of numbers (constants) or variables. If
there are infinite or very many items in the list, we often abbreviate it with
ellipses (...) and subscripts. For example:
• 1,2,3,..., 50 represents the integers from 1 to 50. The ellipsis (...)
indicates
that numbers are left out; they are implicit. We can infer that the missing
values are integers by extrapolating from the values shown.
• 
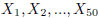represents a series of 50 values. For
example, X might
be a variable measuring the number of sexual partners for each of 50
observations.
• 
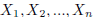represents a list of n things; n may be
variable or unknown.
This is often used to present a general formula that can be applied to any
number of values.
Similar notation is used to represent mathematical operations on a series of
numbers or variables:
• 1 + 2 + ... + 50 indicates that the integers from 1 to 50 are all added
together.
• 1+2+...+n indicates that the integers from 1 to n are all added together;
n is variable or unknown.
• 1 * 2 * 3 * ... * n indicates that the integers from 1
to n are all multiplied
together. (1)(2)...(n) is an equivalent notation.
• 
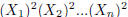indicates that the n variables are squared
and multi-
plied together.
Exercises: Lists
1. What is 2(1)+2(2)+...+2(5)? Hint: There are two things left out where
the ellipsis is.
1.4 Arithmetric and Multiplication
1.4.1 Sums
The simplist way to express a sum is with a plus sign (+). For example, we
can write 1 + 1 = 2. However, when we are summing a series of values, we
sometimes use the greek letter capital sigma (∑) because it allows us to be
much more concise. For example:
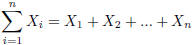
This means that we need to sum the series of numbers
represented by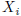 
from
i = 1 to i = n: . For
example, let X be a variable representing
the number of children in a family. Say we have data on three families:
,
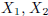and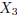 
. We want to know the total number of
children in our data:
When the number of observations (n) is very large, using
the sigma notation is
a much more concise way to express the sum of a series of values. It also allows
us to write general equations for an unspecified n. For example, it is an easy
way to express the formula for the mean of a variable:
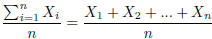
The sigma notation is a very concise instruction to add up
all the values for the
n observations and divide by the sample size (n).
1.4.2 Multiplication
For simple equations, we represent multiplication by 2*2 = 4 or (2)(2) = 4.
When we need to multiply a list of numbers, we use the number capital pi(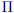
)
to represent the product accross some series. For example:
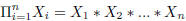
This indicates that we multiply the n values together.
1.4.3 Subtraction and Division
Subtraction is addition of a negative number (2 - 1 = 2 + (-1)) and division is
multiplication by an inverse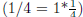 
. Therefore,
subtraction can be repre-
sented by the ∑ notation and division can be represented by the
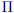notation.
Exercises: Arithmetric and Multiplication
1. What is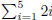 
?
2. What is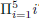 
?
3. What is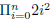 
?
1.5 Convergence and Limits
Convergence means that a sequence or function approaches some limit. Having
a limit means that the function or sequence gets closer and closer to some
value;
this value is the limit. For example:
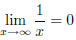
As x → 1, 
→ 0. The
arrow means “converges to” or “approaches.” Here’s
another example:
This function converges to the constant e. So does this sequence:
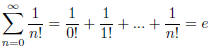
The exclamation point is the factorial (See next section,
1.6).
1.6 The Factorial
The factorial is indicated with an exclamation point (!). The expression n! is
read “n-factorial.” For some number n, n! equals n(n − 1)(n − 2)...(3)(2)(1). 0!
equals 1 by definition. For example:
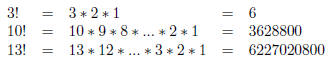
It is easy to calculate factorials using Excel (or another
computer program).
For example, in Excel the foruma “=FACT(n)” gives n!.
The factorial is useful in probability because n! gives you the number of ways
to order n things. Why does this work? There are n things to select for the
first
spot, there are n − 1 things to choose for the second spot, n − 2 things for the
third spot... These selections are independent events so we can multiply their
probabilities: n(n − 1)(n − 2)...
Exercises: The Factorial
1. You’re having a three scoop ice cream cone with three different flavors.
How many ways could you make this cone (eg, how many ways to order
the flavors as first, second, and third scoops)?
2. You also have to choose a cone. There are four types of cones. How many
different combinations of cones and ordered scoops of ice cream are there?
3. You’re organizing your books. You have 3 methods books and 4 theory
books. You want to put all the methods books together and all the theory
books together. All 7 books will be on the same shelf. How many orders
are possible?