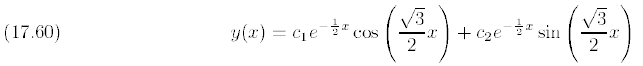Homogeneous Equations with Constant Coefficients, Cont'd
However, this is rarely the form in which one wants a
solution of (17.3). One would prefer solutions that
are real-valued functions of x rather that complex-valued functions of x. But
these can be had as well,
since if z = x + iy is a complex number, then
are both real numbers. Applying the Superposition Principle, it is easy to see that if
and
are two complex-valued solutions of (17.3), then
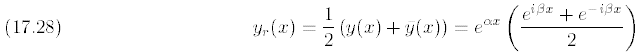
and
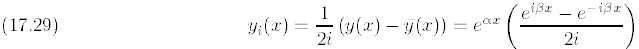
are both real-valued solutions of (17.3).
Let us now compute the series expansion of
and
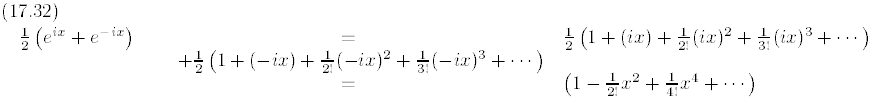
The expression on the right hand side is readily
identified as the Taylor series expansion of cos(x). We thus
conclude
Similarly, one can show that
On the other hand, if one adds (17.33) to i times (17.34) one gets
or
Thus, the real part of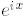 
is cos(x), while the pure
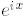imaginary part of is sin(x).
We now have a means of interpreting the function
in terms of elementary functions (rather than as a power series); namely,
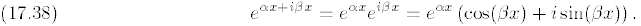
Thus,
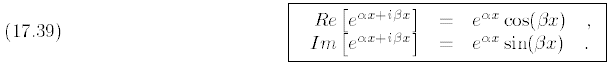
I now want to show how (17.33) and (17.34) allow us to
write down the general solution of a differential
equation of the form
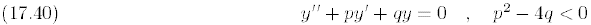
as a linear combination of real-valued functions.
Now when p2 − 4q < 0, then
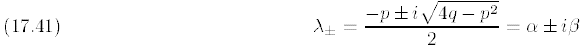
are the (complex) roots of the characteristic equation
corresponding to (17.40) and
are two (complex-valued) solutions of (17.40). But since
(17.40) is linear, since 
and
are solutions so
are
and
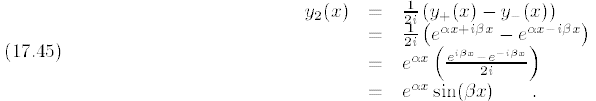
Note that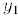 
and
are both real-valued functions.
We conclude that if the characteristic equation corresponding to
has two complex roots
then the general solution is
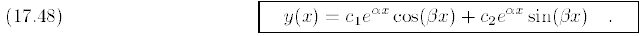
Example 17.1. The differential equation
has as its characteristic equation
The roots of the characteristic equation are given by
These are distinct real roots, so the general solution is
Example 17.2. The differential equation
has
as its characteristic equation. The roots of the characteristic equation are given by
Thus we have a double root and the general solution is
Example 17.3. The differential equation
has
as its characteristic equation. The roots of the characteristic equation are
and so the general solution is
