circle

It is easy to see that the minimum number of posts required is 4. This is because any single light
post will fail to illuminate some great circle. (Imagine that the light post is at the north pole and
the great circle is the equator.) From that point, it is not possible to illuminate that great circle
with less than three additional posts.

The simplest solution, and almost certainly the one with the shortest total post length, comes
from placing the posts at the corners of an inscribed regular tetrahedron as illustrated in Figure 1.
This gives us a total lamppost length of 8R where R is the radius of the planet. The trick is to
prove that this is the minimum length. To do this, we make one clever observation and then use
brute force.

Any minimal lighting solution must correspond to the case of a (not necessarily regular)
tetrahedron inscribed in the circle (this is not the inscribed tetrahedron described in the last
paragraph). This is because the light from a single post creates a circular patch on the sphere that
must contain the “triangular” region given by the space not covered by the other posts. The
minimum post height comes from minimizing the radius of the circle to the one that contains the
three corners of the triangles. The light pattern appears as in Figure 2 below.

We are working in the case of four points at random on a sphere given by x² + y ² + z ² = 1. For
any face of the tetrahedron, we can find a circumscribed circle. The lamppost height
corresponding to that circle is given by similar triangles as illustrated in Figure 3. We see that the
height of the can be found with the help of the ratio

It will be given by the formula

where h′ = h / R and r′ = r / R . At this point, we will just assume a sphere of unit radius. We
make use of the past Puzzle Corner where it was shown that the radius of a circumscribed circle
for a triangle with sides a, b, and c is given by

where K is the area of the triangle. If we use the vectors as given in Figure 4, then the formula
for the areas of those triangles will be given by 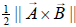etc. This gives us a final formula of

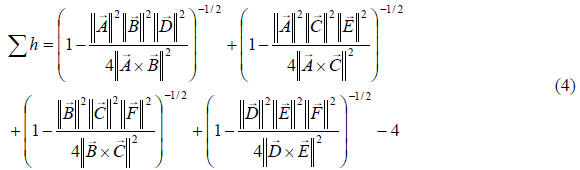
The brute force part comes from generating random inscribed tetrahedrons and determining the
post length that they correspond to. We are solving the problem by throwing darts at it. We pick
the points (without loss of generality, we may pick one point to be the north pole and one point
to be on the x-axis) and check to make sure that the center of the sphere is contained in the
tetrahedron. If it is, we measure the post heights. For instance, for 1,000,000 sets of throws, we
get a minimum height of 8.0497001 and the number of values distributed (for each of 10 equal
intervals) between 8 and 9: 3,9,21,32,47,62,77,88,90,117. This is a clear indication that the
minimum is at 8 (well, clear enough for me).

Figure 1: The minimal lighting solution. The sphere is inscribed in a regular tetrahedron. The
bases of the posts are the corners of an inscribed regular tetrahedron (not shown).

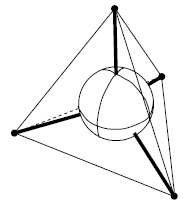
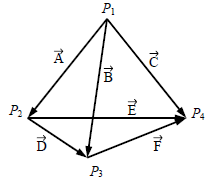
Figure 2: The unlit “triangle” and its circumscribed circle.

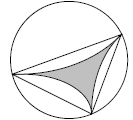
Figure 3: Similar triangles giving the relationship between the radius of a circle (on the surface
of a sphere) and the minimal lamppost height required to illuminate it.

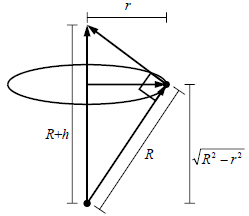
Figure 4: Illustration of the vectors used in Eqn. 4. The points all lie on the surface of a sphere
with radius R.