Basic Algebra Review for Math 1441

6 Complex Fractions

The first step in simplifying complex fractions is to write the numerator as one fraction and
the denominator as one fraction.

Example:

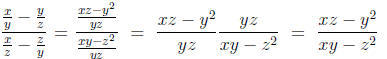
Example:

Here are some to try. Answers are in the solution section.

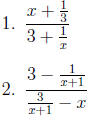
7 Functions

For the function defined by f(x) = 3x - x², we express in English that the function takes a
number, multiplies it by 3 and subtracts its square.

For the function defined by g(x) = 1 - 3x², we express in English that the function takes a
number, squares it, multiplies the result by 3 and subtracts that result from 1.

Here are some for you to try. The answers are in the solution section.

1. If f(x) = 2x - x², find f(x + h) and simplify completely.

2. If 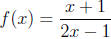find f(x + h) and simplify completely.

3. If f(x) = 3 - 2x², find f(x + h) and simplify completely.

8 Linear Equations

Rewrite the equation so that there are no variables in the denominator and no parentheses.
Move all terms with the variable for which we are solving on one side of the equation and
move all terms without that variable on the other side. Factor out the variable and solve.

Example: Solve 3(x + 2) = 4x + 1 for x: We distribute to get 3x + 6 = 4x + 1. Isolating the
x's on one side, we get 3x - 4x = 1 - 6 or -x = -5. So the answer is x = 5.

Example: Solve 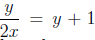   for y: Multiply both sides by 2x to get y = 2x(y + 1) or
y = 2xy + 2x. Isolate the terms with y to get y - 2xy = 2x or y(1- 2x) = 2x. The solution
is

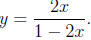
Try the following problems. The answers are in the solution section.

1. Solve

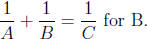
2. Solve A(B + C) = BC + A for C.

9 Quadratic Equations

We can solve quadratic equations by factoring or by using the quadratic equation.

Example: Solve x²-x = 6 by factoring: We put all terms on one side, getting x²-x-6 = 0.
Next, factor to get (x - 3)(x + 2) = 0. If a product ab equals 0, either a = 0 or b = 0. For
our problem, we conclude x - 3 = 0 or x + 2 = 0. The answer is x = 3 or x = -2.

Notice that, if ab = 6, we cannot conclude a = 6 or b = 6. Maybe a = 2 and b = 3 or a =1/2
and b = 12. So, if you factored without moving all terms to one side to get x(x - 1) = 6,
you cannot conclude x = 6 or x - 1 = 6.

Example: Solve x² -x = 6 by using the quadratic formula: Again, we need to put all terms
on one side, getting x² - x - 6 = 0. To solve ax² + bx + c = 0, the quadratic formula tells
us that

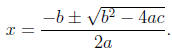
In this example, a = 1, b = -1, and c = -6, so
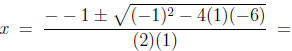
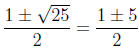. The solution is

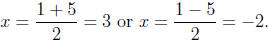
Here are some problems to try. The answers are in the solution section.

1. Solve the equation for x: x² - 2x = 8
2. Solve the equation for x:

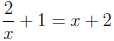
10 Common Mistakes

Remember that For example, 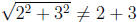since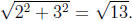
Similarly, 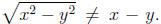However, if x and y are nonnegative, and

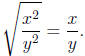
In a similar vein, 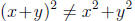since
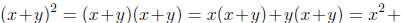
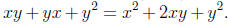. However, 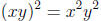since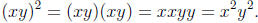
Also,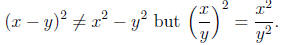
Care needs to be taken when deciding if canceling is possible. We have tha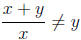t but

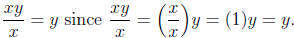
Recall that, for inequalities, if we multiply or divide both sides by a negative number, the
inequality sign gets changed. We know that -3 ≤ 2 but, if we multiply by -2, we get
(-3)(-2) ≥ (2)(-2) since 6 ≥ -4.

Example: Solve 3 - 2x ≤ 9 for x: We get -2x ≤ 9 - 3 or -2x ≤ 6 or x ≥ -3. The answer
in interval notation is [-3;∞).

Example: Solve x + 2 > 4x - 1 for x: We get x - 4x > -1 - 2 or -3x > -3 or x < 1. The
answer in interval notation is (-∞; 1).

Decide if the following statements are true or false. Assume that all variable are nonnegative.
Answers are in the solution section.

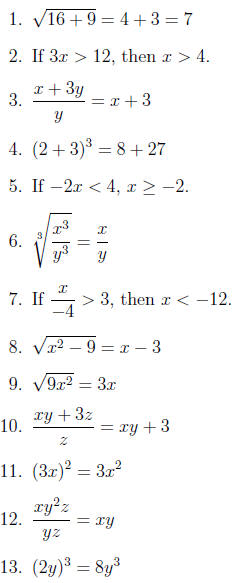
11 Solutions

Section 1:

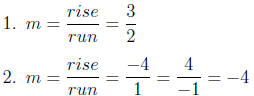
Section 2:
1. 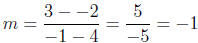and the equation of the line is y - (-2) = -1(x - 4).

2. The points are (3, 0) and (0,-2). So 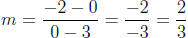and the equation of the
line is

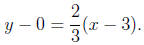
3. To find the slope of the line 2x + 6y = 1, we solve for y: 6y = 1 - 2x so
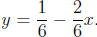
The slope is 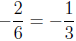and the equation of the parallel line is

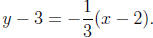
Section 3:

Section 4:

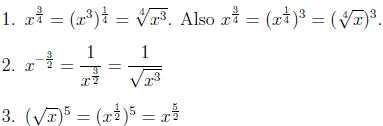
x

Section 5:

Section 6:

Section 7:

Section 8:
1. Multiplying the equation by ABC on both sides, we get BC +AC = AB.
We isolate the terms with B on the left to get BC-AB = -AC. So B(C-A) = -AC
and

2. Distributing, we get AB +AC = BC +A. We isolate the terms with C on the left and
get AC - BC = A - AB. So C(A - B) = A - AB and

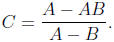
Section 9:

1. x² - 2x - 8 = 0. Factoring, we get (x - 4)(x + 2) = 0 so x - 4 = 0 or x + 2 = 0. The
answers are x = 4,-2.

2. Multiplying both sides of the equation by x, we get 2+x = x² +2x. So 0 = x² + x - 2
and 0 = (x + 2)(x - 1). The answer is x = -2, 1.

Section 10:

1. False:

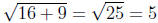
2. True

3. False

4. False: (2 + 3)³ = 5³ = 125

5. False: If -2x < 4 then x > -2.

6. True

7. True

8. False

9. True

10. False

11. False: (3x)² = 9x²

12. True

13. True