Combining Like Terms
| Terms can be classified as “constant terms,”
which have no variable part, or “variable terms,” which have a number and variable part. Constant terms 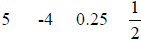 Variable Terms 2x -5y 3x^2 4xy
Terms are expressions which are separated by
addition symbols. |
I like to teach like terms using animals from the barn yard.
If you put 4 goats in a pen and add in 3 more goats, how
many do you have?
4 goats + 3 goats = 7 goats
An algebraic equivalent to this would be:
4x + 3x = 7x
Notice that we did not get 7x^2 . When students ask why,
ask them if we would get 7
goats-squared.
Combing like terms under addition and subtraction is just
like moving animals in and out
of a pen on the farm.
What if you put 4 goats in a pen and add 3 chickens? What
do you get?
(Some irritated critters, for sure!)
4 goats + 3 chickens
= 4 goats + 3 chickens
There is no such thing as a goat-chicken. So, don’t even try it!
An algebraic equivalent to this would be:
4x + 3y
=4x +3y
From these silly examples, we could go into the rule for combining terms.
| Rule: When adding or subtracting, only like terms may be combined. |
If you want to get truly mathematical, the reason stems
from the reverse of the
Distributive Property.
| 4x + 3x | 4x + 3y |
| =x(4+3) | = ? |
| =x(7) | Nothing is in common to reverse the Distributive Property. |
| =7x |
Note: Since we define terms as expressions which
are separated by addition symbols, it
is important for the students to understand that subtracting expressions
actually represent
negative terms.
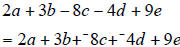
A student could either understand the negative terms as
written, or he could rewrite the
terms, to make things more visually obvious. This is especially important where
the
subtracting negative is concerned.
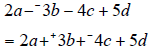
So, just to be safe, students should at least change all
subtracting negative to adding
positives. Then the sign of the term is easy to determine if rewritten or not.
Combine like terms.
(1) 8c +15c
(2) 12h − 4h
(3) 8y − y
(4) w + 7w
(5) 11m −11m
(6) 3a + 4b
(7)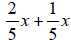
(8) 2.5v + 3.2v
(9) 2x − 9x + 5x
(10) 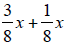
(11) − 6y −17 + 4y + 9
(12) a + 4b − 8b − 5a
(13) − 5v − 4v − 9v + v (
14) 3x + 4(2x +1) + 5
(15) − 5(x + 2) + 4(x − 5)
answers:
(1) 23c
(2) 8h
(3) 7 y
(4) 8w
(5) 0
(6) 3a + 4b
(7) (3/5)x
(8) 5.7v
(9) − 2x
(10) (1/2)x
(11) − 2y − 8
(12) − 4a − 4b
(13) −17v
(14) 11x + 9
(15) − x − 30


