Intermediate Algebra Review #4

The fourth test (Test #4) will occur on Wednesday, December 5, 2007, and will cover §7.1–7.5, 7.7, 7.8; 8.1,8.2 of
the text. That is,

Below are my comments on each of these sections.

It goes without saying—but not without writing—that it is assumed that you have had a good and honest attempt at the
assigned exercises. Pay attention to these problem types, especially the ones that I deemed important enough to grade.
The solutions to the graded problems are located at

Click on the link to the class web site.

As mentioned several times in class, each section has a number of bullet points that encapsulate the important
ideas/techniques. Pay attention to each of these bullet points.
The test itself should be very straightforward, we studied well-defined techniques and problem types. The key is your
ability to factor polynomials. Be sure to cancel all common factors.

Chapter 7: Radical and Rational Exponents

§7.1 n^th Roots and Rational Exponents.
1. Evaluate n^th Roots: We define 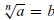provided bⁿ = a. For example 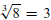. When n is even and
a < 0, 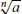is undefined (not a number, or just NaN). When n is an odd integer, then 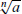always exists. An
important property when n is odd is 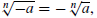, which can be useful in dealing with roots of negative
numbers; thus, .

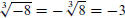2. Simplify 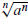: There are two formulas for evaluating 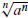. These are
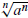= a if n is odd (1)
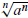= |a| if n is even (2)
For example, 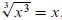, whereas

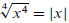
3. Evaluate Expressions 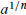: This is the first step towards to definition of rational exponents. We define
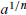to be

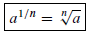
This formula is useful when read from left-to-right (convert for exponential notation to radical notation),
or from right-to-left (convert from radical notation to exponential notation).
A common mistake observed on the homework is not grouping the radicand correctly. For example
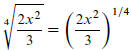however,

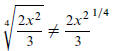
4. Evaluate 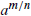: We define

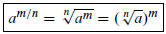
When making numerical calculations, usually, 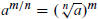is the preferred form for handling rational
exponents, for example,
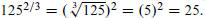
We deal with negative exponents as follows:

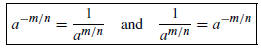
§7.2 Simplify using the Law of Exponents.

1. Using the Law of Exponents: As a general rule, the Law of Exponents are valid for rational exponents.
See the listing of these properties on page 542 in the text. It is assumed that these properties are known to
you.

2. Use the Laws of Exponents to Simplify Radical Expressions: We can use rational exponents and the
Laws to help us work with radicals. Basically, we convert to exponential notation, simplify using the Laws,
the re-convert to radical notation. For example,

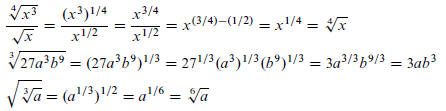
3. Not covered.

§7.3 Simplifying Radical Expressions.

1. The Product Rule for Radicals: This rule is

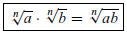
provided the radicals on the left are defined and are real numbers (not complex numbers).
Note that we can only use this rule when the indices of the radical are the same. For example,

2. Use Product Property to Simplify: These are fundamental techniques in this section; this is sometimes
called “extracting roots.”

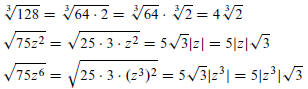
When the index of the root does not exactly divide a power in the radicand, we extract what we can and
leave the rest where it is. For example,

Note, a common mistake is to miscalculate the exact root, the easiest way of doing this is to divide by the
index of the root: 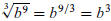. Divide by the index!

3. The Quotient Property: More of the same but with quotients:

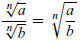
Again, this property is valid only when the roots on the left side all exist and are real numbers (not complex
numbers).

The equation—as with all equations—can be read read left-to-right, or right-to-left. Both directions are
illustrated in this section.

4. Multiply Radicals with unlike indices. Though covered in class, this material will not be on the test.