Matrices, Vectors, and Vector Calculus

• Scalar product. The scalar product between two vectors A and B is defined as

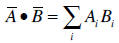
It can be shown that the scalar product as defined above, is equal to the product of the
magnitudes of the two vectors and the direction cosine between them:

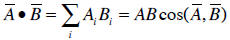
In order to show that the scalar product behaves like a scalar, we must thus show that the
scalar product between A and B is the same as the scalar product between A’ and B’.
The scalar product also satisfies the commutative and the distributive laws:

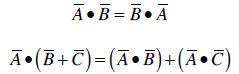
• Vector product. The vector product between two vectors A and B is a third vector C,
defined as

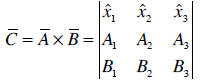
In order to show that the vector product behaves like a vector, we must show that the
vector product transforms like a vector under a coordinate transformation.
The geometrical interpretation of the vector product is shown in Figure 3. The magnitude
of the vector product is the area of the parallelogram defined by the vectors A and B and
it is directed in a direction perpendicular to the plane defined by the vectors A and B
(right-hand rule defines the direction).
There are many properties of the vector product. Some of them are listed here (see the
text book for a more complete listing):

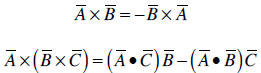
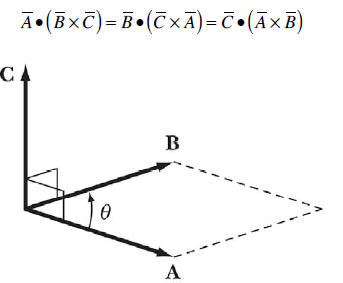
Figure 3. Properties of the vector product between the vectors A and B.

Differentiation and Integration
Two important operations on both scalars and vectors are differentiation and integration.
These operations are used to define important mechanical quantities (such as velocity and
acceleration), and a thorough understanding of operations involving differentiation and
integration is required in order to succeed in this course.

• Scalar Differentiation. We can differentiate vectors and scalars with respect to a scalar
variable s.
o The result of the differentiation of a scalar with respect to another scalar variable will
be another scalar. The result of the differentiation will be independent of the
coordinate system.
o The result of the differentiation of a vector function with respect to a scalar variable
will be another vector. The resulting vector will be directed tangential to the curve
that represents the function.

• Scalar Differentiation in different coordinate systems. An important scalar variable
used in differentiations is the time t. Based on the position vector, we can obtain the
velocity and acceleration vectors by differentiating the position vectors once and twice,
respectively, with respect to time. If the Cartesian coordinates are being used, the axes
are independent of time, and differentiation the position vector with respect to time is
equivalent to differentiating the individual components with respect to time:

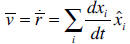
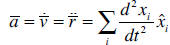
The situation is more complicated if we are using spherical or cylindrical coordinates.
Consider for example the motion of an object shown in Figure 4.

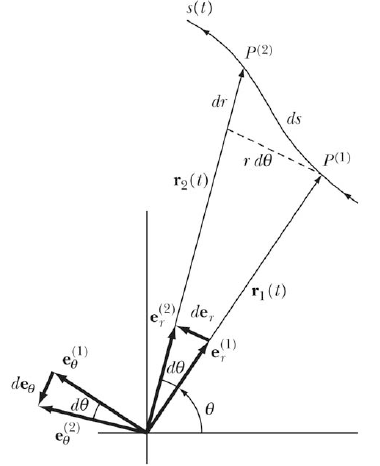
Figure 4. Motion of an object described in terms of spherical coordinates.

When the object moves during a time dt from P(1) to P(2), the spherical unit vectors
change too, as shown in Figure 4:

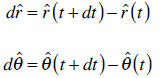
Based on the definition of the unit vectors in the spherical coordinate systems we can
conclude:

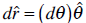
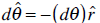
By dividing each side by dt we obtain the following relations:

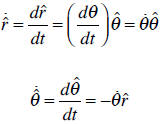
Using these relations we can calculate the velocity and acceleration:

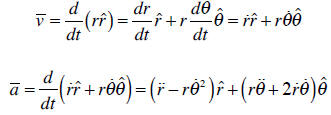
Other relations for spherical and cylindrical coordinates can be found in the textbook.

• Vector Differential Operator. A very important operator in this course will be the
gradient operator. It operates on a scalar function and the result of the operation is a
vector. Consider a scalar function Ø that is a function of the Cartesian coordinates. The
value of the scalar function at a point P in two different coordinate systems must be the
same:

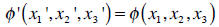
The coordinates in the two different coordinate systems are connected to each other via a
rotation matrix:

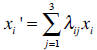
When we differentiate the scalar function we find the following relation:

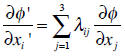
As we can see, the components of the differential of the scalar function transform like a
vector, and the components can thus be considered the components of a vector we call the
gradient of a scalar function:

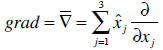
Other important operators are defined in terms of the gradient operator:

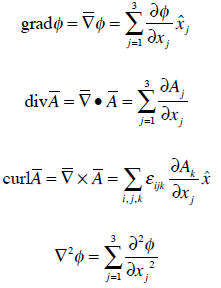
The gradient of a scalar function has the following properties:
o The gradient of a scalar function at a point P is directed normal to the lines or
surfaces for which the scalar function is constant.
o The gradient of a scalar function at a point P is directed in the direction of maximum
change in the scalar function.

• Integration. The opposite of differentiation is integration. Both scalar and vector
functions can be integrated, and we can encounter volume, surface, and line integration:
o Volume integration of a vector. When we integrate a vector over a volume, the
result is another vector with components obtained by volume integration of the
components of the original vector.

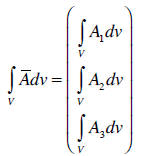
o Surface integration of a vector. The surface integral of a vector function is given by
the integral of its component perpendicular to the surface. When we integrate a
vector over a surface, the result is a scalar.

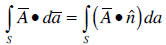
o Line integration of a vector. The line integration of a vector is given by the integral
of the component of the vector along the path (does not need to be a straight line).

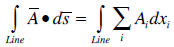
Various theorems relate volume, surface, line integrals of vectors. Some of the most
important theorems are:

o Gauss’s theorem for volume integrals:

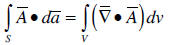
Note: the surface integral of a vector function is replaced by the volume integral of a
scalar function.

o Stoke’s theorem for line integrals:

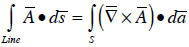
Stoke’s theorem is most useful if it reducing a two-dimensional surface integral to a one-dimensional
line integral.