Mth 111 Test 2 Review
Make sure to do similar problems (such as from the book)
until you are
comfortable with that type of problem!
|
Answer the following questions (1 -5) based on the polynomial P(x) 1. Find P(-5) =
__2___ |
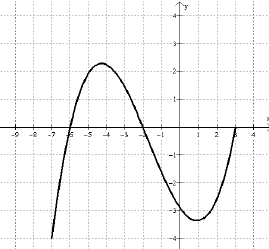 |
5. What are the (x,y) coordinates of the absolute maximum:
__
(-4.5, 2.25)_____
6. The length of a rectangular box is 1 inch more than twice the height of the
box, and the width is 3 inches more than the height. If the volume of the
box is 126 cubic inches, find the dimensions of the box.
Answer: height = 3 inches, width = 6 inches, length = 7 inches
7. Let P(x) = x4 + x3 - x2 + x – 2.
a. Find all the zeros of P(x).
Answer: 1, -2, i, -i
b. Completely factor P(x) into a product of linear terms.
Answer: (x-1)(x+2)(x-i)(x+i)
8. Given 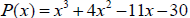
a. Use either long division or synthetic division to show that (x+2) is a
linear factor of P(x).
b. Show that (x+2) is a linear factor of P(x) without using division (hint:
it’s a Theorem).
Answer: P(-2) = 0 (factor thm P.317).
c. Use your results to rewrite P(x) as a product of two factors, one linear
and one non-linear:
Answer: P(x) = (x+2) (x2 +2x -15)
9. Given 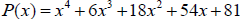 has a zero "-3" with multiplicity
two.
has a zero "-3" with multiplicity
two.
Find the other zeros (real or imaginary). Show your work.
Answer: 3i and -3i.
10. Write a third degree polynomial with zeros 4i and 2 in standard form.
One possible Answer:
![]() .
.
Explanation (nov. 24, 5:30pm) Since 4i and 2 are both roots of the
polynomial,
x-4i and x-2 are both factors of the polynomial, this only gives us a second
degree polynomial though. I
|
11. The graph of P(x) is shown below. a. Write a polynomial in factored form that has the same general shape and the same zeros. One possible answer: (x+3)2(x-1)(x-4) b. What is the degree of P(x)? _ 4 ___ |
 |
12. Given 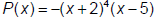 :
:
a. What is the degree of P(x)? __ 5 __
b. What are the zeros of P(x)? __ -2 and 5 _______
c. What is the multiplicity of each zero? -2 has mult. 4 and 5 has mult. 1
d. What is the end behavior of P(x)? up to the left and down to the right
e. Where does P(x) cross the x-axis, if at all? __ at x=5 _____
f. Where does P(x) bounce off the x-axis, if at all? _ at x = -2 ___
13. For each of the functions below determine the horizontal and vertical
asymptotes. If none exist, then write “none”.
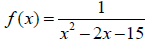 |
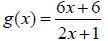 |
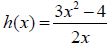 |
|
| Horizontal asymptote: |
x-axis | y = 3 | None |
| Vertical asymptote: |
x = -3 and x = 5 | x = -1/2 | y-axis |
Graph f(x): Use a dotted line to indicate
any asymptotes!

Answer: horizontal asymptote at y=1, vertical
symptote at x=3 (graph on
calculator to check – make sure you label key points!)
|
14. Find the exact polynomial that matches the graph exactly, i.e. it passes through the point (-4,12) and has the same zeros. Answer: 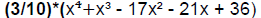 Explanation (nov. 24, 6pm) Since the real roots are -3, 1, and 4, the polynomial has the factors (x+3), (x-1), and (x-4). Since it bounces off at -3, the root -3 has even multiplicity (p. 331). We are told that the equation of the polynomial should have the exact same zeros as the graph. Also, |
 |
|
this graph has the shape of a 4th degree polynomial. Since -3
has even multiplicity, and we have 3 roots so far, 3 must have multiplicity 2. Therefore, our polynomial has the factors (x+3)2, (x-1), and (x-4). We are almost there… we cannot quite conclude that our polynomial is (x+3)2(x-1)(x-4) because we need to make sure it goes through the point (-4,12). So our polynomial may have a leading coefficient of something other than 1. That is our polynomial is of the form p(x)=c(x+3)2(x-1)(x-4), where c is a constant to be determined. Since it goes through the point (-4,12), we know that p(-4)=12. Plugging in -4 for x and setting it all equal to 12 then solving for c gives that c =3/10. So p(x)=(3/10)*(x+3)2(x-1)(x-4) and multiplying out these factors gives the answer above. |
|
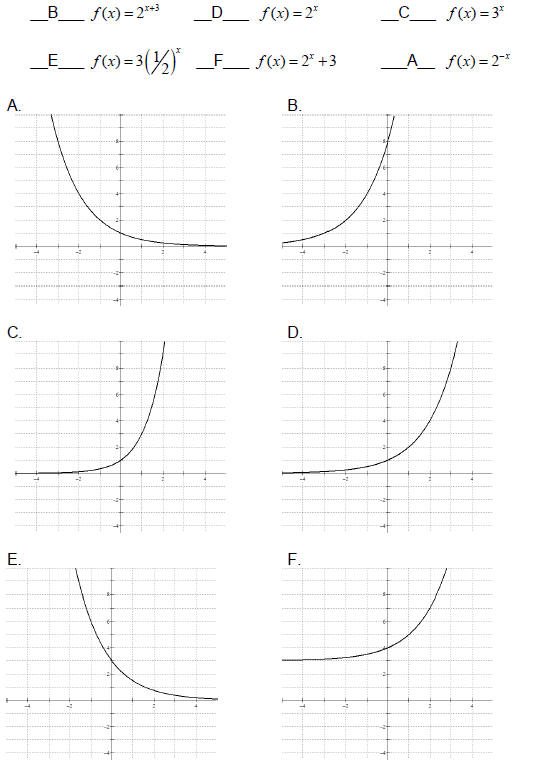
15. Match each function with its graph. Record the letter
of the graph next to the
function.
16. Complete the table below by changing the form of the equation.
| Exponential Form | Logarithmic Form |
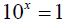 |
Ans: log (1) = x |
Ans: |
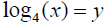 |
17. Write as a single logarithm with a coefficient of 1. Box answer.
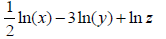
Answer: 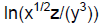
18. Write the logarithm in terms of logarithms x, y, and z. Box answer.
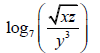
Answer: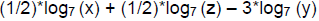
19. Name that inverse! (Find the inverse of each function.)
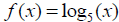 |
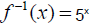 |
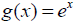 |
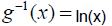 |
20. Calculate 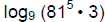 without
a calculator.
without
a calculator.
Answer: 21/2


