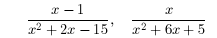Finding and Using Least Common Multiples
1.1 Finding an LCM
The least common multiple (LCM) of two or more polynomials is the polynomial of
least
degree that contains all the factors of each polynomial. To find the LCM, first
factor each
polynomial completely. Then, the LCM is the product of each factor the greatest
number of
times it occurs in any one factorization.
Let’s first take a simple numerical example. Find the LCM of 50 and 60.
First factor.
50 = 2·5·5
60 = 2·2·3·5
The LCM is:
22·3·52 = 300.
Now let’s take a more complicated example. Find the LCM of x2-6x+9
and x2-2x-3.
First factor.
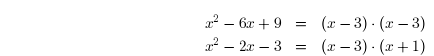
The LCM is:
(x-3)2·(x+1).
No need to multiple it out.
1.2 Using an LCM
The initial purpose of finding an LCM is so that we can rewrite fractions in
terms of least
common denominator (LCD). The basic idea here is that

So if you have a fraction

and you want to rewrite the fraction with another denominator, say 25, just do
this:
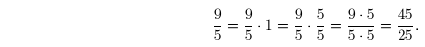
Now let’s take a more complicated example. So if you have a fraction

and you want to rewrite the fraction with another denominator, say 26xy2
, just do this:
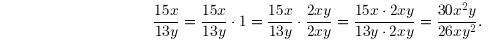
1.3 Examples
1. Find the LCM of the polynomials. 6x2y, 18xy2
2. Find the LCM of the polynomials. 6x2, 4x+12
3. Find the LCM of the polynomials. 8x2(x-1)2, 10x3(x-1)
4. Find the LCM of the polynomials. (2x-1)(3-5x), (2x-1)2(x-5)
5. Find the LCM of the polynomials. x2-2x-24, x2-36
6. Find the LCM of the polynomials. 2x2-7x+3, 2x2+x-1
7. Find the LCM of the polynomials. x2+3x-18, x-3, x-2
8. Find the LCD.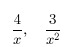
9. Rewrite the fractions in terms of the LCD.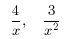
10. Rewrite the fractions in terms of the LCD.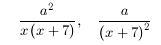
11. Rewrite the fractions in terms of the LCD.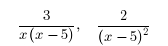
12. Rewrite the fractions in terms of the LCD.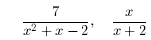
13. Rewrite the fractions in terms of the LCD.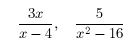
14. Rewrite the fractions in terms of the LCD.